
Passo 1
Vamos entender o problema:
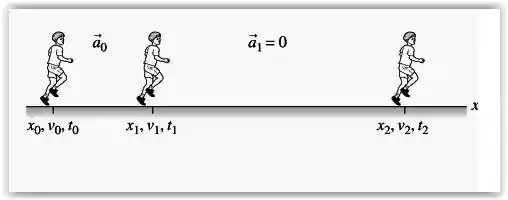
Temos num primeiro momento o corredor com uma aceleração até atingir sua velocidade máxima que se mantem constante, ou seja, a partir desse momento sua aceleração é nula.
Passo 2
Num primeiro momento, temos um movimento acelerado. Então aplicamos a equação da cinemática para esse caso, sabendo que ele parte do repouso:
Para achar o valor da velocidade que ele atinge depois do período de aceleração, ou seja, a velocidade máxima, aplicamos:
Dividindo as duas equações achadas, chegamos a:
Passo 3
Sabemos que o percurso total de 100m do corredor será dado pela soma , ou seja, o que ele percorreu acelerando com o que ele percorreu em 6 segundos (10s – 4s) de forma constante com a velocidade máxima.
Assim montamos:
Do passo anterior achamos quanto vale em função de , então substituímos: