No trânsito de uma cidade podemos observar vários tipos de movimento. Em uma dessas situações encontramos parado em um sinal (farol) o veículo , quando o sinal abre este parte com uma aceleração constante de . Enquanto isso, um veículo , que mantinha uma velocidade constante de , consegue passar pelo sinal aberto mantendo a sua velocidade. Em que posição o veículo se encontra com o veículo , considerando a origem da trajetória como o local onde o sinal está e a estrada retilínea?
(a) ;
(b) ;
(c) Não se encontram;
(d) ;
(e) ;
Passo 1
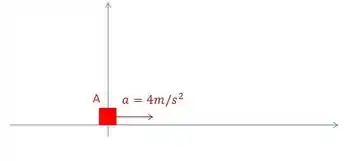
Vamos entender essa situação. A gente tem um semáfaro, aí um carro A teve que parar nele, então no início,
e depois começou a andar quando o sinal abriu. Pra sair do repouso, o motorista tem que pisar no acelerador, a aceleração adquirida foi de
Depois de um tempinho (então o carro A já tinha andando) passa pelo sinal, que ainda tava aberto, um carro B, que nem precisou frear, ele permaneceu com a velocidade dele.
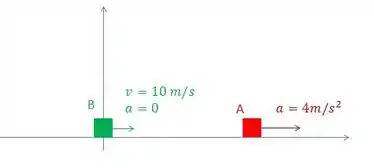
Beleza? Então, o que o exercício tá perguntando pra gente é aonde os carros vão se encontrar.

Maravilha, agora que já entendemos o que tá acontecendo, vamos tirar um dados úteis daí:
Para o carro A tem aceleração, então é um movimento uniformemente variado. Assim, sua posição varia com o tempo da seguinte maneira:
A origem do sistema é o farol, então a posição ali é zero.
E como o carro parou, a velocidade dele no farol era zero também, então:
Substituindo a aceleração que ele deu no enunciado:
Beleza, sabemos como a posição do A varia com o tempo.
Passo 2
Vamos ver o B agora:
O corpo B não muda a velocidade, então o movimento dele é uniforme, ou seja a posição varia com o tempo da seguinte maneira:
A origem é o farol, então a posição inicial é zero. E
Então:
Passo 3
O exercício quer a posição de encontro, ou seja, quando:
Então:
A solução dessa equação pode ser em e . A primeira é quando eles passam pelo farol e a segunda é quando eles voltam a se encontrar.
Então a posição que isso ocorre é:
O encontro ocorre à do farol.
Resposta
Alternativa A