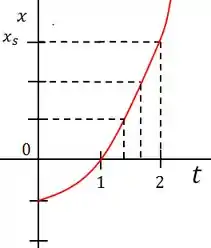
A figura mostra o movimento de uma partícula que se move ao longo do eixo com aceleração constante. A escala vertical do gráfico é definida por . Quais são o módulo e o sentido da aceleração da partícula?
Passo 1
A partícula descreve um movimento retilíneo uniformemente variado já que a aceleração é constante, e portanto segue essa equação aqui.
Como o enunciado definiu a escala vertical do gráfico, temos que cada traço vale , assim descobrimos o valor de
O problema quer saber o valor da aceleração e por isso temos que pegar as informações do gráfico
Pelo gráfico conseguimos obter a posição no início do movimento e nos tempos e .
Passo 2
Para encontrarmos a aceleração vamos usar a equação da posição para dois trechos.
Para começar, vou escolher o trecho entre os tempos e .
Com isso, a equação da posição ficará:
Substituindo esses valores na equação da posição e sabendo que o intervalo de tempo entre essas duas posições vale , ficamos com:
Daqui tiramos a primeira equação.
Passo 3
Agora, vamos olhar para um segundo trecho afim de termos 2 equações.
Eu escolhi olhar para o trecho entre e , onde temos:
Com isso, a equação da posição vai ficar:
Substituindo os valores e lembrando que o intervalo de tempo entre essas posições vale , teremos:
Passo 4
Como queremos a aceleração , e não temos informação de , podemos fazer um sisteminha de equações para cortar e ficarmos só com a aceleração
Multiplicando a primeira equação por e depois fazer a
Chegamos em
A aceleração da partícula é no sentido positivo da trajetória, pois o valor encontrado é positivo.
Resposta
Sentido positivo da trajetória