Seja parte da esfera , com . Calcule a massa de sendo
Passo 1
Cálculo de massa, né? Já vimos que, para achar a massa de uma superfície vamos precisar fazer a integral de superfície dela assim:
Onde já é escrito com as variáveis da superfície parametrizada. Portanto, vamos precisar achar essa parametrização da nossa superfície e calcular o módulo da sua normal. Vamos lá?
Veja que o enunciado diz que a nossa superfície é “parte da esfera ”, que é uma esfera de raio centralizada na origem, nossa parametrização vai ficar assim:
Só que não queremos nossa esfera inteira, vamos ter que limitar , o enunciado também diz que:
Essa restrição acontece somente no intervalo
O ângulo não possui nenhuma restrição, podemos dizer então que
Obs: Outra forma de se obter esses limites é graficamente, nesse caso o esboço seria a superfície da esfera limitada pelo cone
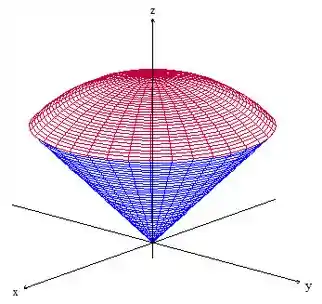
O cone é o limite de , com isso da para dizer que os nossos limites são:
Passo 2
Definida nossa parametrização e nossos limites, vamos ao cálculo do módulo da normal da superfície:
Passo 3
Vamos substituir tudo na integral da massa então:
Onde nossa densidade em função das novas variáveis fica:
Voltando para a integral e substituindo tudo:
Passo 4
Vamos então calcular essa integral
Para integrar em , vamos fazer uma pequena modificação:
Parece que a gente só complicou né? Mas você vai ver que assim a gente consegue integrar, antes, com seno ao cubo não conseguíamos. Voltando pra integral:
A primeira integral é bem simples né?
Na segunda vamos fazer uma pequena alteração:
Juntando as duas: