Esboce o gráfico da função
Passo 1
E aí, galerinha! Tudo na paz por aí?
Vamos precisar seguir nosso roteiro aqui de construção de gráficos que está lá no nosso conteúdo!
Vem comigo que te mostro como vamos conseguir fazer essa questão juntos!!
Passo 2
Primeiro vamos definir qual é o domínio dessa função!
Note que não há divisão por nenhum , logo essa função pode ser dada pelo domínio de todos os reais.
Além disso, podemos perceber que a intersecção dessa função no eixo x e y é zero para ambos. E como sabemos disso? Pra saber onde é a intersecção, basta eu substituir e ver quando dará e depois fazer e ver quanto dá
Passo 3
Nesse próximo passo vamos ver se a função tem alguma paridade, ou seja, se ela é ua função par ou ímpar.
Vamos testar hehe
Logo, a função não é par!
Vamos testar a função ímpar:
Logo, também não é ímpar!!
Passo 4
Agora vamos ver a função tem assíntotas. Vamos começar pelas verticiais. Essas ocorrem perto de pontos de descontinuidade da função, que nesse caso não temos. Então se uma função não tem uma descontinuidade, podemos dizer que não temos assíntotas verticais.
Para as assíntotas horizontais, precisamos pegar a função e fazer e ver se ele vai nos dar um valor limitado diferente de infinito.
Temos indeterminação!! Então precisamos aplicar L’Hôspital!!
Logo, temos uma assíntota horizontal em
Passo 5
Agora vamos ver crescimento da função, analisando o sinal da derivada!!!!
Vamos igualar a derivad a zero e analisar depois o sinal de em relação à raiz encontrada.
Logo, vamos analisar o sinal:
para Crescente
para Decrescente
Passo 6
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos. E como fazemos isso? Basta igualarmos a derivada primeira a zero e achar a raiz e observar o que acontecerá.
Vimos no passo 4 que a muda de sinal, e muda de decrescente para crescente!
Isso significa que temos um mínimo local. Mas podemos descobrir se ele é um ponto de máximo absoluto comparando o valor da função nesse ponto com os valores da função nas fronteiras do domínio.
Vimos que nas fronteiras dos domínios (passo 4) os valores eram e , isso significa que é um mínimo absoluto, pois:
Passo 7
Falta estudar a concavidade da função, e, para isso, precisamos da derivada segunda:
Vamos agora igualar a zero a
Precisamos agora avaliar o sinal da entre esse valor de
para
para
Portanto,
a função tem concavidade para baixo
a função tem concavidade para cima
é ponto de inflexão.
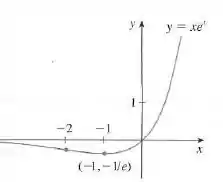
Resposta
Gráfico.