UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 12.
12 - Calcule , onde é a região triangular limitada pela reta e os eixos coordenados.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Aqui nessa questão temos que calcular a integral dupla de dentro da região onde é limitada pelos eixos coordenados e pela reta .
Essa função de integração assusta, não é? 👀
O que estamos fazendo na verdade é calcular o volume de uma caixa triangular com a tampa em um formato que é descrita pela função .
Nesses casos, a primeira coisa que temos que fazer é visualizar a região pra obter os limites de integração.
Se plotarmos as curvas que delimitam , temos
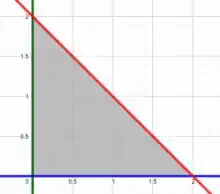
Essa região hachurada em cinza é nossa região !
Interessante, não é? 😁
Passo 2
Agora vamos determinar os limites de integração. Primeiro analisando os limites em , vemos os limites da região na horizontal.
A região é limitada na direita pela reta vermelha e pela esquerda pela reta verde, correto?
Ou seja, limitado pelas curvas e . Isolando em um lado da equação, temos e .
Com isso, nossos limites de integração em é e .
Como já levamos as curvas em consideração, em vamos olhar apenas para os maiores valores que a região atinge.
Com isso, vemos que a região é limitada entre e em , logo esses serão nossos limites de integração.
Portanto nossa integral será da seguinte forma
Mas e aí? Como vamos calcular essa integral? 👀
Passo 3
Se você conseguir, me manda uma mensagem porque você é um mito!
O que podemos fazer para facilitar nossa vida é fazer algumas substituições.
É quase impossível calcular essa integral desse jeito, mas e se substituirmos por e por ?
Com essa mudança, ao invés de calcularmos , calculamos .
Mas então e os limites de integração?
Temos
Como
Então
Se , e limitam nossa região, então para os limites mínimos, temos
E também
Já para os limites máximos, se e , então
No máximo valor em , temos
Dessa forma, nosso é limitado por e .
Um pouco difícil, não é? Mas relaxa, a pior parte já passou!
Passo 4
E nossa função de integração, como fica?
Podemos escrever o expoente de como
Logo nossa função de integração é ou de forma mais simples .
Como fizemos essa mudança de variável, temos que calcular nosso jacobiano. Lembra como calculamos?
Sendo que e
Calculando as derivadas parciais, temos
Calculando o determinante, temos
Como o jacobiano é dado em módulo, então
Com isso, nossa integral é dada finalmente por
Agora já sabemos bem continuar!
Passo 5
Podemos utilizar o método da separação quando temos uma integral dupla onde a função de integração é dada por podemos reescreve-la como . Ou seja
A integral de sabemos que podemos obter pelo método de integração polinomial.
Aplicando os limites de integração
Já a integral de é obtida pelo método da substituição
Aplicando os limites de integração
Calculando o produto dos dois resultados, temos
Questão difícil, não é? Mas conseguimos chegar ao fim!
É isso! Essa resolução te ajudou? Responde Aí! ✌
