Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 481234567891011121314151617181920212223242526272829303132333435363738394041424344454647495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 2a.

2 - Esboce a região de integração e calcule as integrais iteradas a seguir

a) ∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Foi dada uma integral dupla pra calcularmos e desenhar sua região de integração.

Imagine que você tem que encher uma caixa de um liquido que vai salvar o mundo de um desastre e mas na caixa não está escrito o volume que ela tem.

Porém, você sabe que a tampa dessa caixa é dada pela função 2 x + 4 y e sua base é limitada pelas funções y = x e y = 2 x para x variando entre 1 e 0 .

E agora? O que vamos fazer? 🤔

Relaxa, vamos salvar o planeta.

Passo 2

A primeira coisa é ver como é o formato da base dessa caixa que vamos encher.

Sabemos que y varia entre 2 x e x e x entre 1 e 0 . Vamos ver esses gráficos no plano

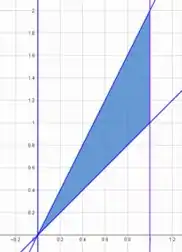
Hachurando do limite superior para o inferior, a área de hachura em comum para x e y é a área da região de integração. Assim como hachurada na imagem de cima!

E o volume da nossa caixa vai ser a integral dupla definida por

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x

Como a integral da soma é a soma das integrais, então

∫ 0 1 ∫ x 2 x 2 x d y d x + ∫ 0 1 ∫ x 2 x 4 y d y d x

Vamos calcular essas derivadas?

Passo 3

Primeiro vamos integrar 2 x com relação a y . Como sabemos a integral de uma constante é igual a constante multiplicada pela variável, já que 2 x se comporta como uma constante quando integramos com relação a y , então

∫ 2 x d y = 2 x y

Aplicando o limite de integração, temos

∫ x 2 x 2 x d y = 2 x 2 x - 2 x x = 2 x 2

Com esse resultado, integramos com relação a x

∫ 0 1 2 x 2 d x

Por integração polinomial, dividimos a variável pela sua potência + 1 e somamos 1 no expoente.

∫ 2 x 2 d x = 2 x 2 + 1 2 + 1 = 2 x 3 3

Aplicando o limite de integração, temos

∫ 0 1 2 x 2 d x = 2 1 3 3 - 2 0 3 3 = 2 3

Com isso, obtemos

∫ 0 1 ∫ x 2 x 2 x d y d x = 2 3

Interessante, não é?

Passo 4

Agora vamos calcular a integral de 4 y com relação a y . Aplicando o método de integração polinomial, temos

∫ 4 y d y = 4 y 1 + 1 1 + 1 = 2 y 2

Aplicando os limites de integração, temos

∫ x 2 x 2 y 2 d y = 2 2 x 2 - 2 x 2 = 6 x 2

Com esse resultado, vamos integrar com relação a x . Também por integração de polinômios

∫ 6 x 2 d x = 6 x 2 + 1 2 + 1 = 6 x 3 3

Aplicando os limites de integração

∫ 0 1 6 x 3 3 d x = 6 1 3 3 - 6 0 3 3 = 6 3

Ou seja, temos

∫ 0 1 ∫ x 2 x 4 y d y d x = 6 3

Tranquilo até aqui?

Passo 5

Recapitulando:

Tínhamos a integral

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x

Dividimos ela em duas

∫ 0 1 ∫ x 2 x 2 x d y d x + ∫ 0 1 ∫ x 2 x 4 y d y d x

Encontramos os resultados

∫ 0 1 ∫ x 2 x 2 x d y d x = 2 3

∫ 0 1 ∫ x 2 x 4 y d y d x = 6 3

Ou seja, o nosso resultado é dado por

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x = ∫ 0 1 ∫ x 2 x 2 x d y d x + ∫ 0 1 ∫ x 2 x 4 y d y d x

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x = 2 3 + 6 3

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x = 8 3

Ou seja, nossa caixa cabe 8 / 3 unidades de medida!

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

∫ 0 1 ∫ x 2 x 2 x + 4 y d y d x = 8 3

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x