USP-SEM CAMPUS- Cálculo 3 – prova 2 – 2022.1
A massa do conjunto cuja a densidade superficial é é:
Passo 1
Olá amiguinho do Responde Aí, está tudo lá em cima?
Essa é uma questão bem típica de integração dupla, na realidade uma aplicação da integral dupla.
Ele te deu a densidade superficial e tu sabe lá da física, se tu tens a densidade superficial e multiplicá-la pela área tu tem a massa.
No matematiques é isso aqui:
Porém nós temos que nossa densidade varia com a posição, logo:
Sendo assim, vamos primeiramente desenhar a região de integração e depois montar a nossa integral, para finalmente resolvê-la.
Iae bora lá?
Passo 2
Para desenhar nosso domínio de integração vamos precisar das seguintes equações:
Todas as questões foram disponibilizadas pelo enunciado da questão.
Desenhando todas, o esboço do gráfico deve ficar algo assim:
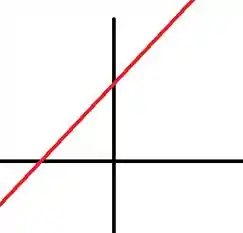
Sendo assim, para encontrar o domínio de integração falta o valor que a função intercepta o eixo , encontrando esse valor de fazendo .
Sendo assim, temos que o domínio de integração ao longo do eixo se torna:
Para encontrar o temos que:
Como notificado no enunciado.
Passo 3
Agora vamos montar nossa integral, temos que a massa é obtida pelo produto da densidade pela área, logo:
Passo 4
Agora precisamos resolver a seguinte integral:
Primeiramente vamos integrar o porque nada nessa integral depende do .
Sendo assim, temos que:
Para resolver vamos realizar a distributiva:
Realizando a integração do polinômio iremos chegar no seguinte resultado
Resposta
Resposta é Letra e)