James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 3 Problema 25.
(Cap 15.3 – Ex 25) Determine o volume do sólido dado.
Abaixo da superfície e acima do triângulo com vértices , e
Passo 1
Falaaaa meus jovens, tudo certinho?
Bora lá?!
Primeiramente vamos analisar a região , que é o triângulo delimitado pelos vértices dados. No plano temos a seguinte região:
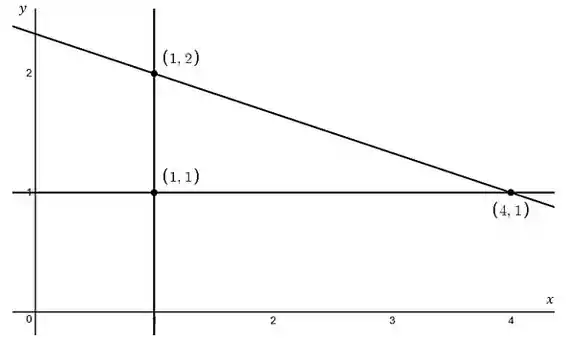
Podemos representar essa área como sendo do tipo I ou II, mas antes de tudo teremos que achar a equação da reta que passa entre e . A sua inclinação é:
E a reta é
Substituindo o ponto :
Então podemos escrever da seguinte forma
Passo 2
Temos então que o volume do solido que é restrito abaixo de na região é dado por
Agora vamos integrar, primeiro em
Agora em relação a
Resposta
Portanto, o volume do sólido é
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x