Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja Ω o domínio representado na figura, onde A é a parte da circunferência x - 3 2 + y 2 = 9 , B é a parte da circunferência x - 1 2   + y 2 = 1 , C é a parte da circunferência x - 4 2 + y 2 = 4 . Reescrever a integral dupla

∬ Ω x + y d A

na forma iterada:

2. vendo Ω   como domínio de tipo 2

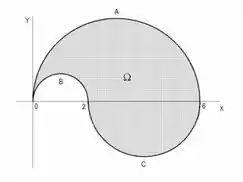
Passo 1

Escrevendo agora como uma do tipo 2 teremos y variando entre constantes e o x variando entre funções. Vamos fazer uma nova separação, mas dessa vez em três regiões:

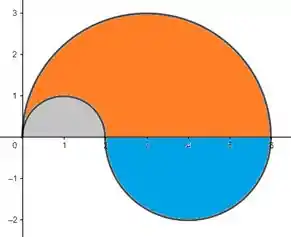
Escreveremos nossa integral fazendo a região azul, mais a região laranja inteira (incluindo a parte cinza), menos a região laranja cinza.

Passo 2

Mas como queremos agora o x variando entre funções, vamos precisar isolar o x nas funções.

A → x - 3 2 + y 2 = 9 → x = 3 ± 9 - y 2

B → x - 1 2   + y 2 = 1 → x = 1 ± 1 - y 2

C → x - 4 2 + y 2 = 4 → x = 4 ± 4 - y 2

Bom, para escrever primeiro a região azul faremos:

∫ - 2 0 ∫ 4 - 4 - y 2 4 + 4 - y 2 x + y   d x d y

Pra descrever a região laranja toda (incluindo a região laranja com a cinza) fazemos:

∫ 0 3 ∫ 3 - 9 - y 2 3 + 9 - y 2 x + y   d x d y

Agora vamos subtrair a região laranja com a cinza:

∫ 0 1 ∫ 1 - 1 - y 2 1 + 1 - y 2 x + y   d x d y

Então totalizando temos:

∫ - 2 0 ∫ 4 - 4 - y 2 4 + 4 - y 2 x + y   d x d y + ∫ 0 3 ∫ 3 - 9 - y 2 3 + 9 - y 2 x + y   d x d y - ∫ 0 1 ∫ 1 - 1 - y 2 1 + 1 - y 2 x + y   d x d y

Resposta

∫ - 2 0 ∫ 4 - 4 - y 2 4 + 4 - y 2 x + y   d x d y + ∫ 0 3 ∫ 3 - 9 - y 2 3 + 9 - y 2 x + y   d x d y - ∫ 0 1 ∫ 1 - 1 - y 2 1 + 1 - y 2 x + y   d x d y

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x