Considere a integral
Onde é a região do primeiro quadrante limitada pelas retas , , e .
Escreva a integral em coordenadas sobre o domínio colocando os domínios de integração explícitos. (Não precisa resolver a integral).
Passo 1
Vamos começar fazendo um esboço dessa região para entender melhor o problema. Temos quatro retas, paralelas duas a duas.
As retas e têm inclinação para a direita (porque tem coeficiente positivo) e cortam o eixo , respectivamente, em e .
As outras duas retas, e , têm inclinação para a esquerda e cortam o eixo em e , respectivamente.
Então, a região é isso aqui:
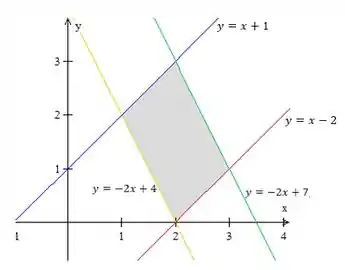
Se você reparar, as retas azul e verde, e se cortam em :
Passo 2
Agora precisamos escrever essa região na integral. Para escrever tanto como tipo I como II, precisamos dividí-la.
Vamos dividir em duas partes em e escrever cada uma delas como tipo I, ok?
Para a parte da esquerda, nós podemos dizer que está entre as retas amarela e azul, e respectivamente. Ou seja, . E, como vemos na figura, .
Para a parte da direita, podemos dizer que varia entre as retas vermelha e verde, e respectivamente. Ou seja, . Pela figura, vemos que .
Passo 3
Agora, vamos levar esses intervalos para as integrais: