Considere a região plana definida por
d) Calcule a área da região plana:
Passo 1
d) Cálculo de área? Integral dupla! Mas, antes, vejamos bem nossa região:
Percebe que ela é parecida com a região , a diferença é que estamos apenas na parte positiva do eixo , ou seja, ela teria metade da área para ! E essa região seria dada por:
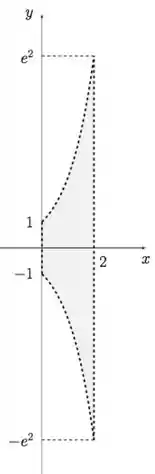
Mas, infelizmente, temos esse terceiro termo aí nos atrapalhando :/
Vamos dar uma olhada nele?
Se o sinal fosse de “igual”, essa seria a equação de uma circunferência centrada em , com raio , certo? Mas, no caso, o sinal diz que o que está do lado direito é maior que esse raio, então estamos na região fora da circunferência! E ainda temos que, como o raio é , o diâmetro é , e ela começa e termina certinho onde começa e termina a restrição do , entre e !
Então, a região que pede-se a área é:
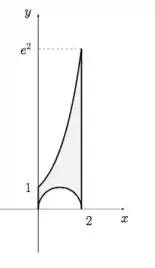
Show? E agora, consegue me dizer qual é o valor dessa área? Antes, sem essa bolota, tínhamos a metade da área de , que pode ser calculada por:
Então, tínhamos . Agora, além de ter perdido essa metade de área, perdemos mais meio disco de raio ! Assim, temos menos metade de , ou seja, menos
Portanto, a área da região é :D
A gente poderia encontrar a área da região direto por integral dupla, só que ia ser beeeem mais complicado. Como é bem tranquilo achar a área de um semicírculo sem precisar integrar fica mais fácil achar a área de e tirar a área do semicírculo 😉
Resposta
d)