Seja uma função contínua em , tal que para todo pertencente a . Considere as seguintes afirmações:
A(s) afirmação(ões) verdadeira(s) para toda função como acima é(são):
Passo 1
1) Como vimos na teoria de inversão de ordem, simplesmente inverter o com o é muito errado! Teríamos que ver a região e mudar os novos intervalos de variação.
No caso da questão acima, ele inverte simplesmente inverte os intervalos...errado
Passo 2
2) Observa que o enunciado afirmou pra gente que certo?
Uma vez que a integral dupla calcula área de quando sendo que área sempre é um valor positivo, garantindo que sempre teremos maior que zero.
Passo 3
3) Pra essa questão eu preciso que você veja comigo o gráfico
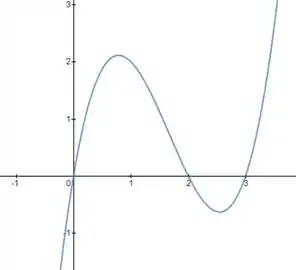
Observa que entre 0 e 3 a integral tem uma inversão, cruzando o . E oque isso significa na prática?
Significa que pra calcular essa integral que o enunciado passa pra gente, essa afirmação:
é errada. O correto seria:
Resposta
Ei, a resposta está no passo a passo :)