1)
- Calcule a massa do sólido
com densidade
Passo 1
Massa de um sólido atualmente é nos dado por uma integral tripla:
Onde para calcularmos, primeiro precisamos colocar na sua forma iterada, ou seja, precisamos descrever . Mas aí surge uma dúvida... Quem é ?
Passo 2
Bem, é a intersecção de duas esferas:
A primeira esfera tem raio e está centrada na origem. Quanto à segunda... Bem, completemos quadrado para você ver o que vai acontecer...
Como ...
Uma esfera também mas deslocada uma unidade em .
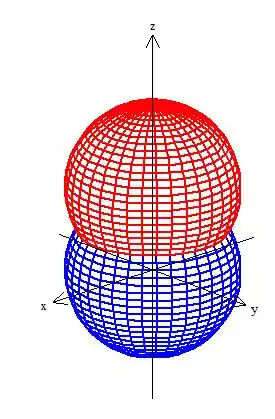
O sólido é o que está acima da azul, mas por baixo da vermelha ;)
Passo 3
Beleza, se estamos trabalhando com esferas, podemos pensar nas coordenadas esféricas:
O jacobiano dessa mudança é...
Ah! E é sempre bom saber que aqui é válida a equação da esfera:
Passo 4
Para determinar os limites das novas variáveis, pensemos no seguinte:
O nosso sólido é esse cara daqui:
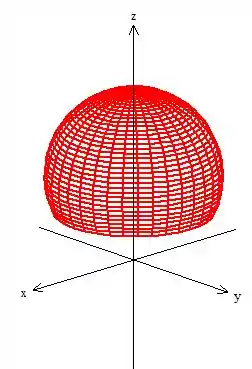
Como é o ângulo que varia em cima de e (porque na mudança usamos o apenas em e ), olhemos para o sólido projetado no plano ...
Repare que dá uma volta inteira para formar o círculo, então...
Quando a variável , o ângulo que desce no eixo ...
Bem, ele tem que estar variando de até o encontro de uma esfera com a outra, ou seja, até a intersecção. Como as equações de ambas são...
Logo
Como o raio nesse encontro é o raio da esfera menor, ou seja, ...
Logo, o ângulo máximo de variação de é ...
Quanto ao , basta substituir na inequação dada no problema...
Passo 5
Antes de voltar para a integral, apenas não esqueça de substituir a mudança de coordenada na função densidade:
Passo 6
Montando então a integral tripla não se esquecendo do Jacobiano...
Agora é só integrar ;)
Fazendo uma substituição...