Considere a função tal que
onde
e a integral tripla
a) Esboce corretamente a região , indicando no desenho a sua fronteira.
b) Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas esféricas . (Neste item não é pedido o cálculo da integral.)
c) Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas . (Neste item não é pedido o cálculo da integral.)
d) Calcule .
Passo 1
Resolvendo a letra a) da questão:
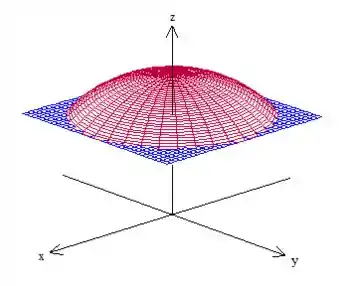
Temos uma esfera centrada na origem de raio e um plano que a corta, o problema se refere à região compreendida entre essas duas superfícies:
Passo 2
Resolvendo a letra b) da questão:
Para descrever a região em coordenadas esféricas, faremos a seguinte substituição nas equações das superfícies:
Para a esfera:
Para o plano:
Como os valores de variam desde a superfície do plano até a da esfera, temos . Como a região faz uma volta completa em torno de , sabemos que . Para encontrar o intervalo de , vamos fazer a interseção entre as superfícies:
Como varia desde o eixo , onde até , temos:
Passo 3
Agora vamos escrever a função em coordenadas esféricas:
Passo 4
Reescrevendo a integral em coordenadas esféricas, temos:
Não se esqueça do fator de conversão
Passo 5
Resolvendo a letra c) da questão:
Para descrever a região em coordenadas cilíndricas, faremos a seguinte substituição nas equações das superfícies:
Para a esfera:
Temos, portanto . Pela imagem, vemos que , uma vez que o sólido está envolta do eixo de simetria .
A equação do plano não muda, continua . Como o valor máximo de é no topo da esfera, onde , temos . Assim, podemos descrever a região como:
Você também poderia ter escrito a região como tipo I, fazendo e , porém, encontraria uma integral mais complicada e teria que usar substituições trigonométricas para resolvê-la.
Passo 6
Vamos, agora, escrever a função em coordenadas cilíndricas:
Passo 7
Reescrevendo a integral em coordenadas cilíndricas, temos, então:
Não se esqueça do fator de conversão .
Passo 8
Resolvendo a letra d) da questão:
Faremos a substituição: