Questão 2: Seja e considere
Seja a integral
- Escreva usando coordenadas cilíndricas .
- Escreva usando coordenadas esféricas .
- Calcule para .
Passo 1
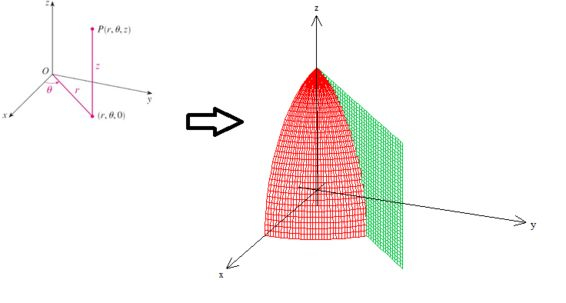
Primeiro vamos desenhar o nosso sólido para termos uma visão geométrica do problema, ok?
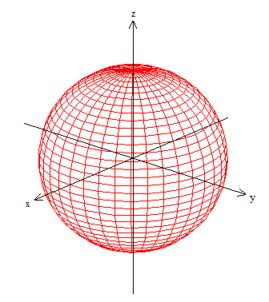
ORA! , trata-se do interior de uma esfera de aio qualquer...
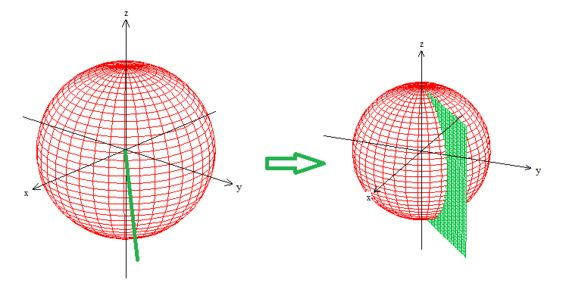
é um plano que dá pra desenhar primeiro riscando a reta no plano e depois puxando pra cima...
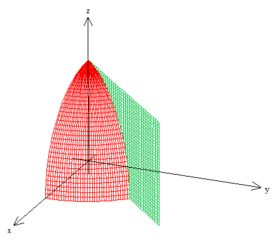
Como e , o nosso é apenas a metade desse gomo de vermelho aqui:
Passo 2
Letra A)
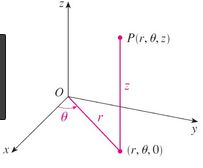
Para descrever esse cara em coordenadas cilíndricas, devemos nos lembrar de que...
Onde o , e o variam dessa forma aqui:
Passo 3
Comparando o nosso sólido com a forma de variação das variáveis novas...
Podemos perceber que a altura entra no por baixo em e sai por cima na equação da esfera...
Então...
Enquanto que o e o variam na projeção do sólido no plano . Tal projeção, por se tratar de uma esfera em cima de ...
Isso aí é a equação de uma circunferência de raio , então a projeção no plano é...
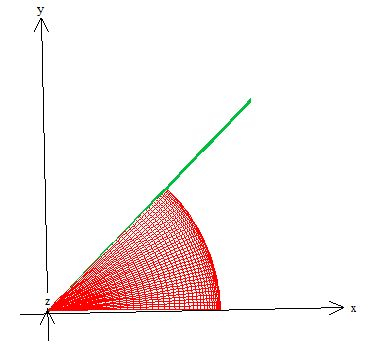
Veja que o está variando de ate a reta ...
Como
Então
Por último, basta observar que o é o raio na região que vaia de até o raio máximo que é ...
Passo 4
Escrevendo a integral então nessas coordenadas...
Passo 5
Letra B)
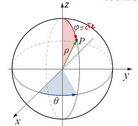
Nas coordenadas esféricas, no entanto, devemos fazer...
Onde as coordenadas ariam dentro de uma esfera...
Passo 6
Para encontrar os limites dessa coordenadas aí no nosso sólido a gente deve comparar:
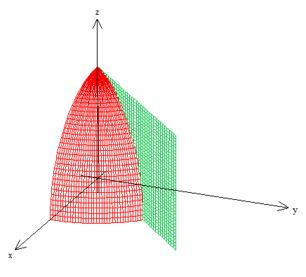
Veja que dessa vez o varia de até o raio da esfera máxima:
Enquanto isso, ângulo continua variando de até ...
Já o ângulo varia de até o plano fazendo um ângulo total de ...
Passo 7
Novamente montando a integral, mas dessa vez nas coordenadas esféricas...
Passo 8
Letra C)
Vamos escolher uma das integrais e trabalhar com ela, ok? Vamos escolher a primeira:
Lembrando que ...
Podemos separar essa integral aí em duas:
Passo 9
Vamos calcular a primeira delas...
Fazendo uma mudança como essa daqui:
Não se esquecendo de trocar também os limites de intgeração...
Então...
Pow: ...
Fazendo outra mudança...
Logo...
Passo 10
Vamos fazer continhas semelhantes para essa integral aqui
Com a mudança...
Então...
Novamente, estamos considerando ...
A última mudança que vamos fazer é...
Passo 11
Podemos concluir então que...
Resposta
Letra a)
Letra b)
Letra c)