Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Séries de Taylor

Ver Teoria
Exercício 671234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666869707172737475767778798081828384858687888990919293949596979899100

Enunciado

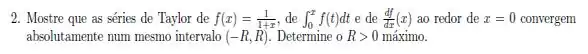
Passo 1

Bom, primeiro vamos reescrever f ( x ) de maneira esperta!

f x = 1 1 + x = 1 1 - ( - x )

Agora ficou fácil encontrar a série de Taylor dessa função, não é?

Sabemos que:

∑ n = 0 ∞ x n =   1 1 - x

Vamos “trocar” x por - x então:

1 1 + x = ∑ n = 0 ∞ - 1 n x n

Pronto, vamos agora encontrar a integral e a derivada dessa função para depois encontrarmos o raio de convergência, ok?

Passo 2

Primeiro vamos derivar:

d f d x = d ∑ n = 0 ∞ - 1 n x n d x = ∑ n = 0 ∞ - 1 n n x n - 1

Agora vamos integrar:

∫ 0 x f ( x ) d x = ∫ 0 x ∑ n = 0 ∞ - 1 n x n d x =   ∑ n = 0 ∞ - 1 n x n + 1 n + 1  

Pronto, encontramos as séries das funções pedidas. Agora basta encontrarmos o raio de convergência de cada uma, certo? Para isso vamos usar (de novo hehe) o critério da razão.

Passo 3

Então, temos que, pelo teste da razão a convergência se da:

lim n → ∞ ⁡ c n + 1 c n < 1

Assim, para a função temos:

c n = - 1 n x n

c n + 1 = - 1 n + 1 x n + 1

Então, temos o seguinte limite:

lim n → ∞ ⁡ - 1 n + 1 x n + 1 × 1 - 1 n x n < 1 ⇒ x < 1

Logo R = 1

Passo 4

Agora para derivada da função temos:

c n = - 1 n n x n - 1

c n + 1 = - 1 n + 1 ( n + 1 ) x n

Então, temos o seguinte limite:

lim n → ∞ ⁡ - 1 n + 1 ( n + 1 ) x n × 1 - 1 n n x n - 1 < 1 ⇒ x < 1

Logo R = 1

Passo 5

Agora para a integral da função temos:

c n = - 1 n x n + 1 n + 1

c n + 1 = - 1 n + 1 x n + 2 n + 2

Então, temos o seguinte limite:

lim n → ∞ ⁡ - 1 n + 1 x n + 2 n + 2 × n + 1 - 1 n x n + 1 < 1 ⇒ x < 1

Logo R = 1

Assim, o raio de convergência é o mesmo para todas as funções.

Resposta

Exercícios de Livros Relacionados

Demonstre que a série obtida no Exercício 11 representa x para todo x .
Encontre a série de Taylor de f centrada em 4 se f n 4 = - 1 n n ! 3 n n + 1 Qual é o raio de convergência da série de Taylor?
Encontre a série de Maclaurin f ( x ) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n → 0 .] Também encontre o raio de converg
Use a série binomial para expandir a função como uma série de potência. Diga o raio de convergência. 1 1 + x 4
Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada. f x = sen ⁡ π x