IME, Cálculo 1, 2021, VF, Q1A
- Calcule o volume do sólido gerado pela rotação, em torno do eixo x, do conjunto de todos os pares tais que e .
- Esboce no mesmo plano os gráficos das polares e , calculando a área da interseção entre elas.
Passo 1
Faaala, pessoal! É sempre interessante ter uma noção dos gráficos de funções elementares como as hiperbólicas. Dito isso, o primeiro passo para calcular volume de rotação é desenhar a área rotacionada:
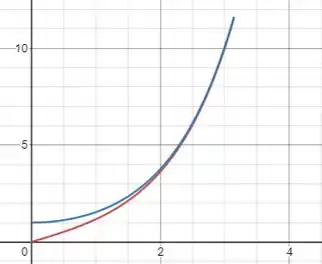
Vamos trabalhar com o conceito de discos finos. O volume da rotação de tal área em torno do eixo é:
Onde o raio do disco são as funções hiperbólicas.
Passo 2
Assim,
Porém, a identidade fundamental:
Nos permite escrever:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .