Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 531234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515254555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

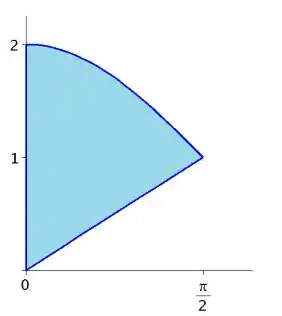
Questão 3:

Considere a região plana R definida por:

R = x ,   y ∈ R 2   |   0 ≤ x ≤ π 2 , 2 x π ≤ y ≤ 1 + cos ⁡ x

Seja S o sólido de revolução obtido pela rotação de R em torno do eixo x .

  1. Esboce abaixo a região plana R .
  2. Utilizando o método que preferir, escreva o volume de S como uma integral ou como uma soma de integrais.

    3. Obs.: Neste item não é necessário calcular o volume.

  3. Calcule o volume de S .

Passo 1

Para esboçar a região vamos fazer o seguinte:

  1. Desenhar cada equação dada nas inequações...

x = 0

x = π 2

y = 2 π x

y = 1 + cos ⁡ x

Bem, as duas primeiras trata-se de retas paralelas ao eixo y :

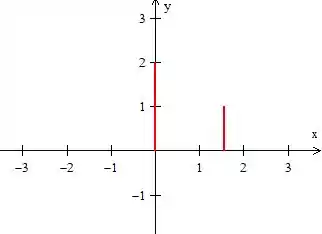
A terceira equação, também é uma reta afinal 2 / π é um número...

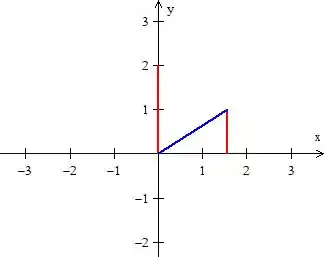
Quanto a última equação, me acompanha com mais calma!

Passo 2

Conhecemos o gráfico de y = cos ⁡ x .

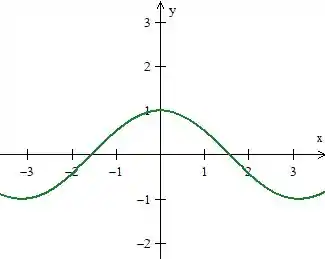
É essa senoide passando por y = 1 quando x = 0 . Quando somamos um com ela, deslocamos todo o seu gráfico pra cima em uma unidade:

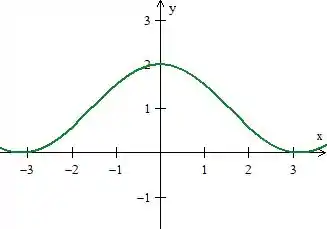
Passo 3

Colocando essas 4 curvas juntas

já somos capazes de ver a região R ali na intersecção delas!

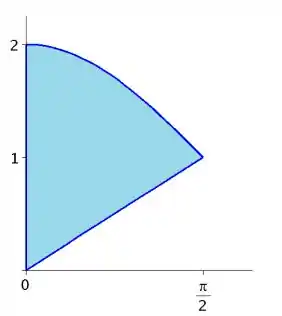
Para o seu gráfico ficar bonitinho, repare que aquele ponto de encontro lá no meio do plano é o π 2 ,   1 , pois se substituirmos o π 2 na função cosseno...

y = 1 + cos ⁡ π 2 = 1

Sacou? :D

Passo 4

b )

Como estamos rotacionando a ao redor do eixo x , é melhor fazermos pelo método dos discos. Nesse método:

V o l = π ∫ a b f x 2 - g x 2 d x

O que precisamos basicamente é saber quem é f x ,   g x ,   a e b .

Passo 5

Vamos começar desvendando os limites de integração.

Esses limites é de onde x começa até o limite máximo do sólido ao redor de x . Observamos que:

a = 0

b = π 2

Passo 6

Quanto às funções, a função f x é sempre a que está por cima, no caso ela é a função cosseno:

f x = 1 + cos ⁡ x

Já a g x a função que está por baixo...

g x = 2 x π

Pegando esses 4 caras e voltando para a fórmula...

V o l = π ∫ a b f x 2 - g x 2 d x =

π ∫ 0 π 2 1 + cos ⁡ x 2 - 2 x π 2 d x =

π ∫ 0 π 2 1 + 2 cos ⁡ x + cos 2 ⁡ x - 4 π 2 x 2   d x

Passo 7

c )

Basta resolver essa integral aí em x :

π ∫ 0 π 2 1 + 2 cos ⁡ x + cos 2 ⁡ x - 4 π 2 x 2   d x =

π ∫ 0 π 2 1 + 2 cos ⁡ x - 4 π 2 x 2   d x + π ∫ 0 π 2 cos 2 ⁡ x   d x

Essa primeira integral sai tranquilo...

π x + 2 sin ⁡ x - 4 π 2 ⋅ x 3 3 0 π 2 + π ∫ 0 π 2 cos 2 ⁡ x   d x =

π π 2 + 2 - 4 π 2 ⋅ π 2 3 3 + π ∫ 0 π 2 cos 2 ⁡ x   d x =

π π 2 + 2 - π 6 + π ∫ 0 π 2 cos 2 ⁡ x   d x

Calculando agora essa outra integral lembrando que podemos fazer a troca trigonométrica:

cos 2 ⁡ x = 1 + cos ⁡ 2 x 2

Então...

π 2 + π 3 + π ∫ 0 π 2 1 2 + cos ⁡ 2 x 2   d x =

π 2 + π 3 + π 1 2 x + sin ⁡ 2 x 4 0 π 2 =

π 2 + π 3 + π 1 2 ⋅ π 2 = π 2 + π 3 + π 4 =

2 π + 7 π 2 12

Resposta

a )

b ) ∫ 0 π 2 π 1 + 2 cos ⁡ x + cos 2 ⁡ x - 4 π 2 x 2   d x

c )   2 π + 7 π 2 12

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .