Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 611234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Q01V) Encontre o volume do sólido obtido pela rotação da região entre as curvas y = x 2 + 3 , x = 2 , x = - 2 e y = 2 em torno da reta y   =   1 .

Passo 1

Essa questão vai ser um pouco difícil de fazer sem ajuda gráfica. Então vamos ver que curvas temos:

y = x 2 + 3

x = 2

x = - 2

y = 2

Opa, só uma parábola e retas! Fica até um pouco mais tranquilo de desenhar assim! Como multiplicando o x 2 na parábola temos um número positivo, ela é daquelas com concavidade pra cima. Um esboço bom do gráfico da região que essas curvas fecham é:

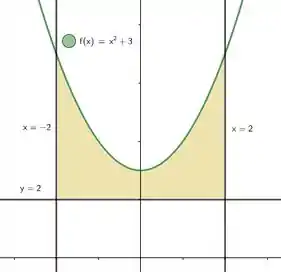
Mas olha, queremos essa região rotacionada não ao redor do eixo x e sim ao redor de y = 1 :

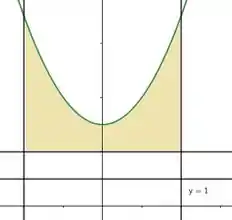
Vamos dividir essa região em 2 pra ficar mais fácil de entender, ok? Vamos ter a área A :

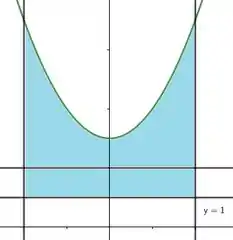
E a área B :

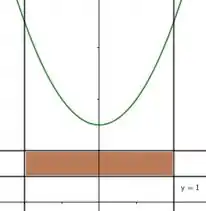
Oras, se a região que queremos é igual à região A - B , então o volume do sólido gerado pela rotação de A em torno de y = 1 menos o volume do sólido gerado pela rotação de B em torno de y = 1 nos dá a resposta! Vamos calcular então esses volumes separadamente.

Passo 2

Começando por A , seja o método dos discos dado por:

V A = ∫ a b π R x 2 d x

Como A está delimitado entre x = - 2 e x = 2 , esses vão ser os limites de integração, beleza?

V A = ∫ - 2 2 π R x 2 d x

Quanto ao raio do disco R x , dá uma olhada:

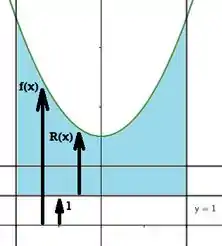
O raio sempre parte do eixo de rotação até a curva, para todos os valores de x definidos na região. Sendo o eixo de rotação uma unidade menor do que o valor de f x , para qualquer x que se tome, teremos:

f x = R x + 1

R x = f x - 1

E logo:

V A = ∫ - 2 2 π f x - 1 2 d x

Como f x nesse caso é a equação da curva, temos:

V A = ∫ - 2 2 π x 2 + 3 - 1 2 d x = ∫ - 2 2 π x 2 + 2 2 d x

Agora é só calcular:

V A = ∫ - 2 2 π x 2 + 2 2 d x = ∫ - 2 2 π x 4 + 4 x 2 + 4 d x

V A = π x 5 5 + 4 x 3 3 + 4 x x = - 2 x = 2 = π 2 5 5 + 4 . 2 3 3 + 4 . 2 - - 2 5 5 + 4 - 2 3 3 + 4 - 2

V A = π 32 5 + 32 3 + 8 - - 32 5 - 32 3 - 8 = π 32 5 + 32 3 + 8 + 32 5 + 32 3 + 8

V A = π 64 5 + 64 3 + 16 = π 192 1 5 + 320 15 + 240 15 = π 192 15 + 320 15 + 240 15

V A = 752 π 15

Passo 3

Agora, partindo pra B , seja o método dos discos dado por:

V B = ∫ - 2 2 π R x 2 d x

Pra achar R x agora vamos fazer a mesma coisa:

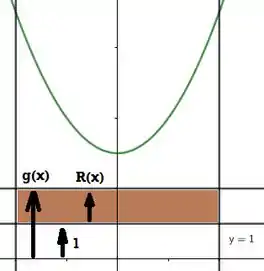
O raio sempre parte do eixo de rotação até a curva, para todos os valores de x definidos na região. Sendo o eixo de rotação uma unidade menor do que o valor de f x , para qualquer x que se tome, teremos:

f x = R x + 1

R x = f x - 1

E logo:

V B = ∫ - 2 2 π f x - 1 2 d x

Como f x nesse caso é uma reta horizontal y = 2 , temos:

V B = ∫ - 2 2 π 2 - 1 2 d x = ∫ - 2 2 π 1 2 d x = ∫ - 2 2 π   d x

Agora é só calcular:

V B = ∫ - 2 2 π   d x = π x x = - 2 x = 2 = 2 π - - 2 π = 2 π + 2 π = 4 π

Passo 4

Pra fechar com chave de ouro falta só juntar os resultados. Como o volume que o enunciado pede é:

V = V A - V B

Vamos ter:

V = 752 π 15 - 4 π

V = 752 π 15 - 60 π 15

V = 692 π 15

Resposta

V = 692 π 15

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .