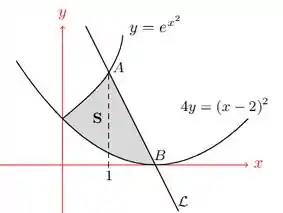
Na figura abaixo, seja o ponto de interseção da curva e a reta , e seja o vértice da parábola . Suponha que a reta passa pelos pontos e .
Calcule o volume gerado pela rotação da região sombreada em torno do eixo-.
Passo 1
Temos o esboço da região a ser rotacionada em torno de , mas não temos a função da reta . Logo, isso é a primeira coisa que temos que achar.
A equação genérica da reta é dada por . Temos dois pontos pertencentes a reta e, tcharan(!), uma reta é definida por dois pontos. Logo, é só substituirmos o e pelas coordenadas dos pontos para acharmos a reta.
Depois, iremos calcular o volume de revolução. Repare que vamos ter que dividir a área em duas. Além disso, como queremos rotacionar em torno de , vamos usar as funções em função de e não de . Assim:
Passo 2
Achando as coordenadas de :
Achando as coordenadas de :
Achando a equação da reta :
Fazendo :
Logo:
Passo 3
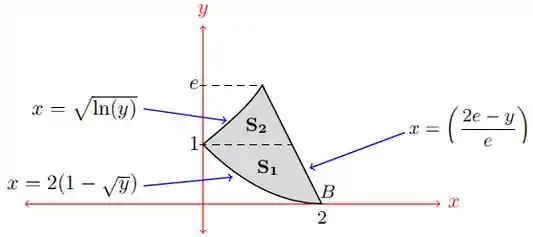
Colocando as funções em função de :
Como , temos as seguintes curvas:
Vamos dividir a região em duas regiões da seguinte maneira:
Passo 4
Vamos calcular através de integrais:
Vamos calcular a integral do final pelo método da integração por partes (repare que aparece uma função logarítmica e um ).
Substituindo em :
Calculando a área total:
Resposta
O volume é igual a