UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 10
A região sob o gráfico de no intervalo é girado em torno do eixo . Encontre o volume do sólido gerado.
Passo 1
Bom dia, boa tarde, boa noite, boa madrugada! Vamos resolver mais uma questãozinha?
Para facilitar a nossa vida vamos dar uma olhada na região que nos foi pedida, beleza? Temos o seguinte:
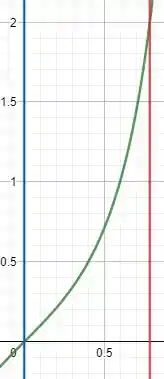
A curva verde representa nossa função, e as linhas azul e vermelha representam os limites estabelecidos. Se rotacionarmos isso em torno do eixo vamos obter o seguinte gráfico:
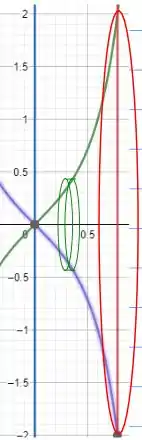
Note que eu deixei em evidência um pequeno disco de espessura e raio dado pela função . Portanto, vamos tentar usar o método dos discos para calcular o volume deste sólido de revolução! Belezinha?
Passo 2
O método dos discos é tal que o volume será dado por:
Integral assustadora neh? Mas tem algumas identidades que vão facilitar a nossa vida! Primeiro vamos lembrar que:
E que:
De forma que temos:
Não parece que melhorou muito! Mas na verdade, isso é a nossa salvação! Vem comigo!
Passo 3
Se usarmos que:
Temos que:
Isso parece feio! Mas por incrível que pareça, podemos resolver por substituição simples! Saca só!
Passo 4
Se considerarmos que e em ambas as integrais, temos:
De forma que podemos identificar as primitivas para obter:
Ou voltando para a variável original:
Aí está nosso volume! Bora para a próxima hehehehe! Tchauzinho!
