Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 661234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

4. Seja R a região do plano delimitada pelas curvas y = tan ⁡ x , x = π 3 e y = 0 . Determine o volume do sólido S de revolução obtido da rotação de R em torno da reta y = 2 .

Passo 1

Oi, galerinha! Tudo bom? Aqui nós temos uma questão de calculo de volume. Ou seja, vamos ter que integrar para encontrar o volume deste sólido S .

Para quem não lembra a fórmula de volume para um sólido de revolução, usando o método dos discos, é

V S = π ∫ a b r ( x ) 2 2 - r x 1 2 d x

Então vamos desenhar a figura para entender quais os limites de integração deste sólido e as funções que o limitam também.

Bora lá!

Passo 2

Desenhando todas as curvas indicadas no enunciado ficamos com

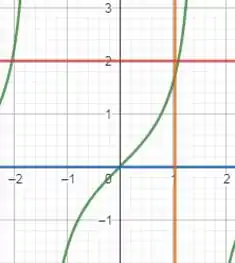
Repara que o nosso sólido varia em x de x = 0 até x = π 3 . E o raio em y vai variar de y = tan ⁡ x até y = 2 .

Ou sejan temos que,

r x 2 = 2

E

r x 1 = 2 - tan ⁡ x

Logo, a nossa integral ficará assim,

V S = π ∫ 0 π 3 [ 2 2 - 2 - tan ⁡ x 2 d x

V s = ∫ 0 π 3 4 tan ⁡ x - tan 2 ⁡ x d x

Agora bora integrar!

Passo 3

Repara que temos uma integral trigonométrica para resolver,

V S = π ∫ 0 π 3 4 tan ⁡ x - tan 2 ⁡ x d x

Então vamos usar a relação de tangente e secante. Lembra que

tan 2 ⁡ x = sec 2 ⁡ x + 1

Logo,

V S = π ∫ 0 π 3 4 tan ⁡ x - sec 2 ⁡ x + 1 d x

Resolvendo essa integral, ficamos com,

V S = π - 4 ln ⁡ cos ⁡ x - tan ⁡ x + x 0 π 3

V s = π 4 ln ⁡ 2 - 3 + π 3

Prontinho!

Resposta

V s = π 4 ln ⁡ 2 - 3 + π 3

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .