UFU, Sem Campus, Cálculo 2, P1 - 2022.1, Questão 1.
1 – Calcule o volume do solido de revolução obtido pelo giro da região limitada por , , e em torno do eixo .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão estamos interessados em calcular o volume do solido que é gerado a partir da rotação em torno do eixo da região limitada pelas equações , , e .
Tem ideia de como fazemos isso? 👀
A primeira coisa a se fazer é visualizar como é essa área limitada por essas curvas e a partir daí escolher qual o melhor método que podemos usar.
Já adianto que o que vamos usar é o método dos discos.
O volume de um disco é dado por
Onde é o raio e é a altura.
Vamos guardar essa informação, por enquanto.
Passo 2
Se esboçássemos a região que vai gerar nosso solido, vamos obter algo mais ou menos assim:
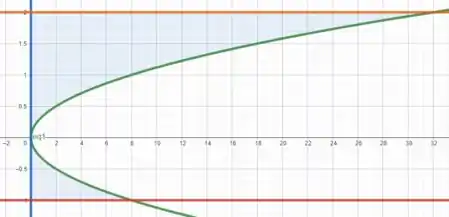
Perceba que ao rotacionar em torno do eixo , a região desenvolverá um movimento circular em torno de .
Assim, se dividíssemos a altura em valores infinitesimais , teríamos infinitos discos de altura e raio , consegue ver isso?
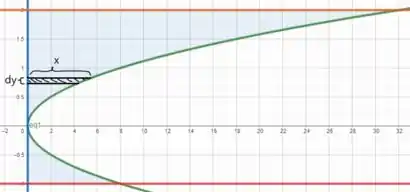
Então, dessa forma, cada volume infinitesimal dessa região será dado por
Onde agora é o raio e é a altura.
é dada pela curva verde
Integrando os dois lados de e substituindo por , temos
Estamos interessados apenas em variando entre e , logo
Tranquilo até aqui? 😎
Passo 3
Pelo método de integração polinomial, temos que
Aplicando os limites de integração
Substituindo em
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
