UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 8
Determine o volume do sólido obtido pela rotação da região, no segundo quadrante, limitada pela curva , inferiormente pelo eixo e à esquerda pela reta , em torno da reta .
Passo 1
Fala aí galera, tudo bom?
Nessa questão precisamos calcular o volume de um sólido de revolução. Ou seja, o volume de um sólido que é obtido pela rotação de uma região plana em torno de um eixo.
No caso desse exercício, a região plana está no segundo quadrante e é limitada pelas curvas:
E, o eixo de rotação é a reta ...
Pois é gente, a rotação não é em torno do eixo ou , mas em torno da reta .
Na prática, isso não vai mudar taanta coisa assim. Para calcular volume de sólidos de revolução, podemos usar o método das cascas, segundo ele:
Porém, essa expressão é válida quando rotacionamos em torno do eixo . Como aqui iremos rotacionar em torno do eixo , precisamos ajustar o termo que representa a distância até o eixo de rotação. Assim:
Massa! Agora que ajustamos a integral, vamos identificar melhor a nossa região que está sendo rotacionada para depois calcularmos o seu volume de revolução.
Passo 2
Nossa região está no quadrante e é limitada pelas curvas:
A primeira curva é o gráfico de uma equação cúbica, em que é a única raiz real, pois:
Assim, o seu gráfico tem o seguinte formato:
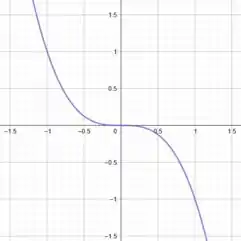
Já as outras duas curvas são mais simples.
é o próprio eixo .
é uma reta vertical passando pelo ponto .
Adicionando as curvas no mesmo gráfico, e analisando o segundo quadrante, temos:
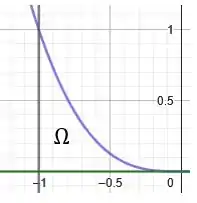
Perfeito! Essa é a nossa região que será rotacionada.
Passo 3
Agora que já conhecemos essa região, podemos finalmente montar a integral correspondente ao volume do sólido de revolução, .
Vimos no passo que:
Como a nossa região vai de , temos que . Logo, podemos tirar o módulo:
Como se trata da região abaixo da curva , temos:
Logo:
Colocando para fora do integrando:
Então:
Ufaaa! Matamos mais uma questão. É isso pessoal, obrigado pela atenção. Até a próxima 😊