Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ. Cálculo 1. Prova P2. 2022.1. Questão 2.

2 – Seja R a região do plano limitada pelas curvas y = 2 x - x 2 e y = x . Seja S o sólido de revolução obtido após girar em torno do eixo x . Calcule o volume de S .

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão, temos duas curvas, a primeira é dada por y = 2 x - x 2 , já a segunda é dada por y = x . Entre essas curvas, se forma uma região.

Se revolucionarmos essa região em torno do eixo x , vamos obter um solido S . Nosso objetivo aqui é calcular o volume desse solido S .

Tem ideia de como fazer isso? 🤔🤔

Nesses casos, podemos usar o método dos discos! Ao revolucionarmos uma área ao redor de um eixo, podemos dizer que a área infinitesimal é dada por

A = π R 2

Cujo o volume infinitesimal é dado por

d V =   π R 2 d x

Sendo que R é o raio do disco que justamente é dado pela função f x

Portanto, o volume total é dado por

V = ∫ a b π f x 2 d x

O que nos resta é adaptar esse conceito ao nosso problema!

Bora lá? 😁

Passo 2

Vamos começar esboçando as curvas y = 2 x - x 2 e y = x no plano para obter os limites de integração a e b .

Igualando as duas funções

2 x - x 2 = x

x 2 = x

Para satisfazer essa igualdade, x pode ser 0 ou 1 , então, confirmando o esboço que obtemos, nossos limites de integração são 0 e 1 .

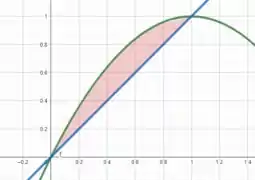
Perceba que a área que estamos interessados é dada pela área abaixo da curva verde y = 2 x - x 2 menos a área abaixo da curva azul y = x .

Portanto, quando formos calcular a integral de revolução para obter o volume, temos que calcular o volume dado pela curva verde e subtrair o volume dado pela curva azul.

Vamos começar a montar nossas integrais!

No caso, nosso raio é dado por y e a altura é dada por d x .

Reescrevendo as equações, temos

y 1 = 2 x - x 2

y 2 = x

Assim, como nosso raio está variando entre y 1 e y 2 , nossa integral fica como

V = ∫ 0 1 π y 1 2 - y 2 2 d x

Tranquilo até aqui? 😉

Passo 3

Substituindo y 1 e y 2 na integral, temos

V = ∫ 0 1 π 2 x - x 2 2 - x 2 d x

Calculando 2 x - x 2 2 , temos x 4 - 4 x 3 + 4 x 2

V = ∫ 0 1 π x 4 - 4 x 3 + 4 x 2 - x ² d x

V = ∫ 0 1 π x 4 - 4 x 3 + 3 x 2 d x

Podemos colocar o π pra fora da integral, já que é uma constante

V = π ∫ 0 1 x 4 - 4 x 3 + 3 x 2 d x

Assim, pelo método de integração polinomial somando 1 no expoente da variável e dividindo a variável pelo resultado da soma do seu expoente, temos

∫ x 4 - 4 x 3 + 3 x 2 d x = x 4 + 1 4 + 1 - 4 x 3 + 1 3 + 1 + 3 x 2 + 1 2 + 1 = x 5 5 - x 4 + x 3

Aplicando os limites de integração...

∫ 0 1 x 4 - 4 x 3 + 3 x 2 d x = 1 5 5 - 1 4 + 1 3 - 0 5 5 - 0 4 + 0 3 = 1 5

Substituindo esse resultado em V

V = π ∫ 0 1 x 4 - 4 x 3 + 3 x 2 d x

V = π 1 5

V = π 5

Portanto, o sólido de revolução que estávamos procurando tem π / 5 unidades de volume!

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

V = π 5

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .