UFRJ – Cálculo 1 – 2020.2 – P4 – Exercício 8
Seja o sólido comum a duas esferas, cada qual com raio , cujos centros distam entre si. O volume de é
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Nesse problema vamos brincar um pouco com o uso de integrais para calcular o volume de sólidos de revolução.
Você deve ter aprendido que é possível calcular o volume de uma esfera pensando na rotação da região limitada pela curva e a reta em torno do eixo , o que é dado pela integral
Nesse problema vamos usar essa ideia, mas para calcular o volume comum (interseção) a duas esferas de raio cujos centram distam . Para fazer isso, vamos considerar duas circunferências de raio , uma centrada na origem e a outra no ponto . As equações dessas circunferências são
Isolando em cada uma, achamos
A seguir desenho as duas curvas:
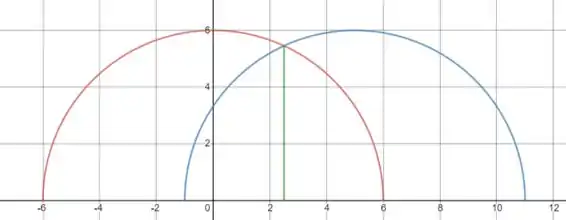
Em vermelho temos a curva e em azul a curva . Para achar a intersecção entre as curvas (ponto na extremidade da reta verde), fazemos
Isso nos leva a
Passo 2
O volume do sólido pedido será dado pela soma do volume do sólido obtido pela rotação da região abaixo da curva azul com entre e com o volume do sólido obtido pela rotação da região abaixo da curva vermelha com entre e . Pela simetria do problema, os dois volumes são iguais, de modo que podemos escrever
As duas integrais vão nos dar a mesma resposta. Vamos calcular a primeira que é um pouquinho mais simples:
Portanto,
Assim,
Logo,
Daí, é só assinalar a alternativa A 😊.
Resposta
Alternativa A.