UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 6c
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região do primeiro quadrante limitada à esquerda pelo círculo , à direita pela reta e superiormente pela reta .
Passo 1
Ooi pessoal, tudo bemm?
Nesse item devemos determinar o volume de um sólido obtido pela rotação da região limitada pelas curvas:
Pra calcular esse volume, após identificarmos melhor a região de integração, podemos usar o método das cascas. Vocês lembram o que ele diz?
Basicamente, o volume obtido pela rotação da região abaixo da curva é:
Show de bola! Então, vem junto comigo para gente aplicar esse raciocínio 😊
Passo 2
Primeiramente, vamos identificar melhor quem é essa região que está sendo rotacionada. Ela é delimitada pelas curvas:
Sabemos, pelo enunciado, que a equação:
corresponde a um círculo. Além disso, esse círculo está centrado na origem do plano e possui raio igual a .
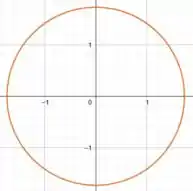
Mas, devemos lembrar que estamos interessados apenas no quadrante. Ou seja, na região em que .
As outras duas curvas que delimitam a região são retas constantes.
é uma reta horizontal passando por .
é uma reta vertical passando por .
Assim, plotando todas essas curvas em um mesmo gráfico e analisando apenas o quadrante, temos:
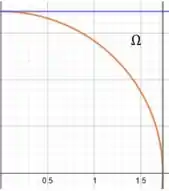
Prontinho gente! Já conseguimos visualizar a nossa região , que será rotacionada.
Passo 3
Agora vamos usar o método das cascas pra montar as integrais.
Aqui é bem importante a gente perceber que, como a região está limitada entre duas curvas, não conseguimos calcular o volume gerado por ela em uma única integral.
Precisamos pensar no seu volume como uma operação do volume gerado pela região abaixo da curva da circunferência, e pelo volume gerado pela região abaixo da reta . Assim:
Volume obtido pela rotação da região abaixo da reta
Volume obtido pela rotação da região abaixo da circunferência.
Inclusive, falando nisso...precisamos de uma equação que represente a curva para podermos aplicar o método das cascas. Como podemos fazer isso com a curva vermelha do círculo?
Já que a equação da circunferência é:
Podemos isolar :
E, como estamos no quadrante, . Logo:
Excelente! Vamos então usar:
E montar as integrais para e .
Para , temos , e a curva está no intervalo de a . Logo:
Já para como vimos agora há pouco, e o intervalo de integração também vai de a . Portanto:
Show de bola! Falta apenas calcularmos essas integrais.
Passo 4
Começando pelo cálculo de :
Colocando as constantes para fora da integral:
Resolvendo a integral monomial:
Excelente! Vamos agora para :
Novamente colocando as constantes para fora:
Para resolver essa integral precisaremos fazer uma mudança de variável. Chamando:
E, quando :
quando :
Ajustando a integral para a substituição:
Fazendo mudança de variáveis:
Logo:
Boaaaa! É só substituir na equação para e correr pro abraço:
Então:
Uhuuuul! Finalizamos mais uma.
Todo mundo conseguiu acompanhar até aqui? Responde Aí!