Calcule o volume do sólido de revolução obtido a partir da rotação de
Em torno do eixo .
Passo 1
Vamos esboçar isso aí antes de tudo. Vou traçar primeiro e , que são mais simples de serem desenhados. Aí substiuirei quando e .
O gráfico ficará assim:
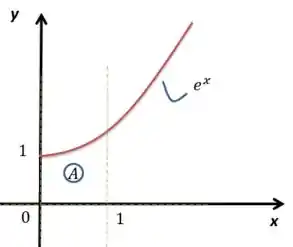
Aquele ali representa a área que eu vou girar em torno do eixo .
Bom, o raio de rotação da figura será , nesse caso. Então a integral a ser feita vai ser:
Passo 2
Integrando essa moleza aí:
E é isso, pessoal.