Questão 5) Considere a região limitada pelas curvas e no intervalo . Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Passo 1
Bem, o volume de um sólido formado girando por uma curva ao redor de pode ser calculado pelo método dos discos...
Onde o que basicamente devemos fazer é procurar quem são os termos dessa integral e calcula-la. Então vamos nessa?
Passo 2
As funções e são as funções que estão por cima e por baixo respectivamente. Mas agora quem poderão ser elas? Ora, basta que desenhemos a região indicada no enunciado:
é uma curva que delimita e também (em azul)
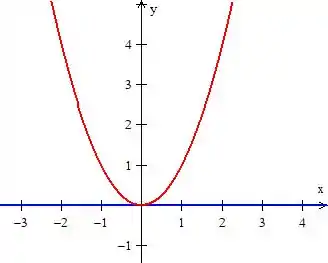
Como varia de a , a região é essa daqui:
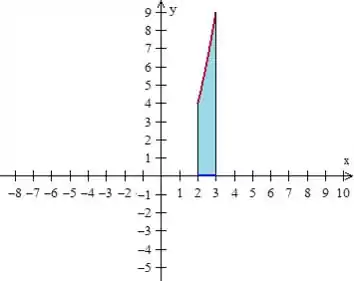
Repare que a função que está por cima é a parábola, logo...
Enquanto a ...
Logo...
Passo 3
Para e , bem basta ver que os limites de é de e , então...
Passo 4
Só calcular: