Seja a região delimitada pelas curvas ,
a) Esboce a região
b) Determine a área da região
c) Seja o sólido obtido pela rotação da região ao redor da reta . Expresse o volume por uma ou mais integrais.
d) Calcule o volume de
Passo 1
a) A região é a região verde esboçada abaixo.
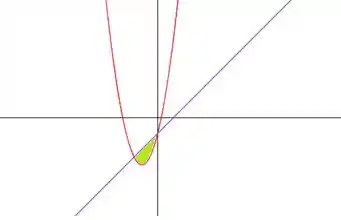
Os pontos de interseção ocorrem quando
Entao as coordenadas dos pontos de interseção são e .
Passo 2
b) A área de pode ser calculada por meio de uma integral definida que tem como limites de integração os pontos de interseção das duas curvas, isto é, e . Como na região a curva é maior que a curva a integral que representa a área terá a seguinte cara:
E agora é só resolver:
Passo 3
c) Observe o esboço abaixo
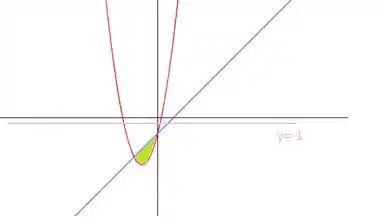
Ao rotacionar a área R em torno de formaremos anéis cujos raios são:
Como o eixo de rotação, como é e não , o raio de rotação não vai ser a própria altura da função e sim menor. Estando o eixo de rotação afastado de uma unidade do eixo :
Se entendermos a região verde como a subtração da azul pela bege:
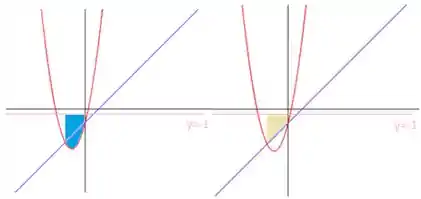
Achamos o volume da região verde subtraindo o volume da região azul rotacionada pelo volume da bege rotacionada. Como para a região azul é e pra bege é , temos:
Passo 4
d) O volume vai ser descoberto resolvendo a integral encontrada anteriormente.
Resposta
Ei, a resposta está no passo a passo :)