Unicamp, Física 3, 2019.2, P2, Teste 1.
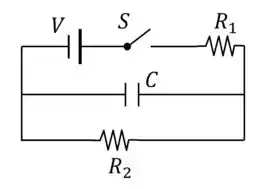
O capacitor no circuito da figura está inicialmente descarregado. Um longo tempo depois que a chave foi fechada, a diferença de potencial através de é:
a)
b)
c)
d)
e)
Passo 1
A chave dessa questão está naquele trecho do enunciado: “um longo tempo depois”.
O que acontece depois que o capacitor fica um longo tempo ligado na fonte de tensão? Ele fica totalmente carregado!
E quanto o capacitor está totalmente carregado, ele se comporta como uma chave aberta. Então é como se o circuito ficasse assim:
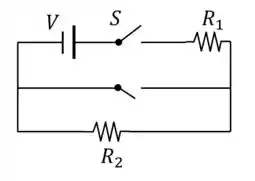
Passo 2
Então ficamos com um circuito bem simples, só com dois resistores em série.
Nesse caso, a resistência total do circuito é:
E então a corrente (que é a mesma em todos os pontos do circuito) é:
Então a diferença de potencial no resistor é, pela lei de Ohm:
Substituindo com a fórmula para a corrente :
Resposta
Letra (c).