Na figura temos um circuito formado por duas baterias, dois resistores, um capacitor e uma chave . Inicialmente a chave está aberta por um tempo muito longo.
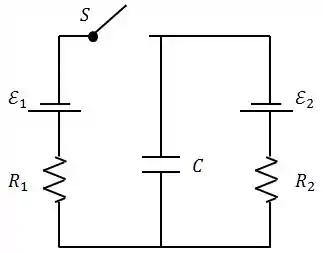
Nesta situação, determine a carga no capacitor ;
A chave é então fechada e mantida assim por muito tempo, determine:
As correntes nos resistores e ;
A diferença de potencial entre as placas do capacitor;
A variação da carga nas placas do capacitor.
Passo 1
Nesta situação, determine a carga no capacitor ;
Inicialmente, pra facilitar um pouco o nossa vida, vamos definir a malha da esquerda como malha 1, e a malha da direita como malha 2.
Nesse primeiro instante, com a chave aberta por um tempo muito longo, o único circuito que importa é a malha 2.
Repare que o problema disse que a chave está aberta por um tempo muito longo... assim, devemos considerar o capacitor como totalmente carregado. Logo, nesse caso, a carga no mesmo será dada por:
Passo 2
Determine as correntes nos resistores e ;
Agora a chave foi fechada e mantida assim por um tempo muito longo. Logo, novamente o capacitor está completamente carregado. Neste caso, não há corrente no ramo do capacitor, de forma que, eliminando o ramo do capacitor, resta somente a malha contendo os resistores e e as fontes e .
Finalmente, utilizando a Lei das Malhas de Kirchhoff, teremos:
Passo 3
Determine a diferença de potencial entre as placas do capacitor;
Vamos definir 2 pontos e no circuito.
dodi0216
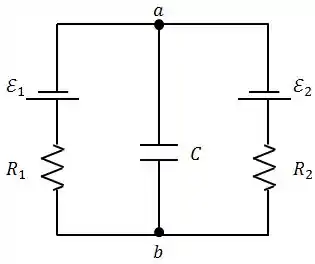
A diferença de potencial entre esses dois pontos deve ser a mesma, independente do percurso que seja escolhido para analisar o circuito.
A diferença de potencial entre as placas do capacitor será justamente a diferença de potencial entre os pontos e . Assim, vamos calcular essa diferença de potencial através do ramo que possui a fonte e o resistor .
Substituindo a expressão que encontramos no item anterior, teremos;
Passo 4
Determine a variação da carga nas placas do capacitor.
A carga no capacitor na situação inicial foi dada por:
A carga no capacitor na situação final será dada por:
Assim, a variação de carga será:
Resposta