No circuito da figura, as chaves e estão inicialmente abertas e não há corrente no circuito. Dados: , , , , , . .
a) Calcule a resistência equivalente e a capacitância equivalente do circuito.
b) Se somente a chave é fechada, calcule a corrente em cada resistor. Desconsidere a resistência interna da fonte.
A partir daqui, considere apenas o circuito equivalente. Suponha que o capacitor equivalente está inicialmente descarregado e apenas a chave é fechada, criando um circuito .
c) Deduza a expressão da carga (medida em ) em função do tempo (medido em ).
d) Qual será a carga máxima armazenada no capacitor equivalente.
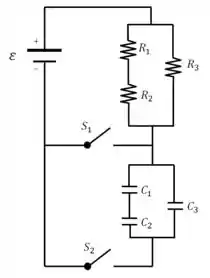
Passo 1
(a) Vamos começar olhando para aquele trecho que tem os resistores. A ideia aqui é encontrar a resistência equivalente:
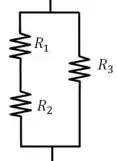
Os resistores e estão em série, então eles podem ser trocados por um único resistor , cuja resistência vai ser:
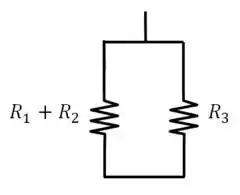
Beleza, agora ficamos com dois resistores em paralelo. Lembra da fórmula para encontrar a resistência equivalente nesses casos?
Agora é só resolver essa soma:
Invertendo os dois lados:
E substituindo os valores numéricos:
Passo 2
Agora vamos fazer a mesma coisa para a capacitância equivalente:
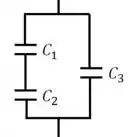
Os capacitores e estão em série. A capacitância equivalente de dois capacitores em série segue essa fórmula aqui:
Resolvendo essa soma:
Invertendo os dois lados:
E então:
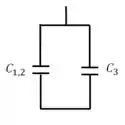
Agora temos dois capacitores em paralelo. Nesse caso é só somar as capacitâncias para encontrar a capacitância equivalente:
Substituindo os valores numéricos:
Passo 3
(b) Quando somente a chave é fechada, o circuito envolve só a fonte e os resistores:
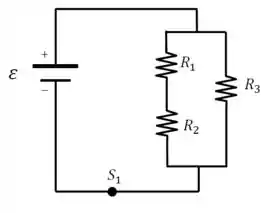
O nosso objetivo aqui é calcular a corrente em cada um dos resistores.
Então o primeiro passo é saber qual é a corrente total que transita pelo circuito. Pra isso a gente pode aproveitar a resistência equivalente que calculamos lá em cima.
Pela lei de Ohm:
Como os resistores e estão em série, a corrente que passa por eles é a mesma:
Ou seja, nós só temos duas variáveis aqui: e , então precisamos de duas equações. A primeira equação nós já temos, porque se a corrente total no circuito é , então:
Já a segunda equação a gente pode encontrar usando a lei das malhas:
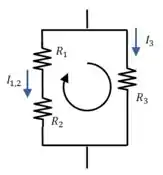
Percorrendo a malha nesse sentido, a contribuição de cada resistor para a integral vai ser sua resistência multiplicada pela corrente que passa por ele, então:
E a corrente aparece com um sinal negativo porque está no sentido contrário ao que escolhemos para percorrer a malha.
Ok, ficamos com um sistema de duas equações:
Passo 4
Vamos resolver esse sistema. Primeiro reorganizamos um pouco:
Substituindo os valores numéricos:
Dividindo a segunda equação por :
E substituindo a segunda na primeira:
E substituindo isso na segunda equação:
Beleza, então as correntes que passam por cada resistor são:
Passo 5
(c) A partir de agora, o enunciado pediu para pensarmos somente no circuito equivalente, e com apenas a chave fechada, ou seja:
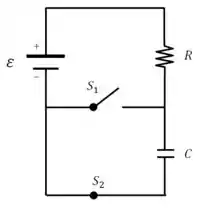
Ok, o enunciado quer que a gente deduza a expressão para a carga no capacitor em função do tempo.
Bom, o primeiro passo pra encontrar essa fórmula no circuito é usando a lei das malhas.
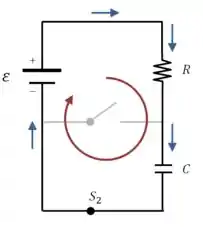
A contribuição da fonte para a integral é , a do capacitor é e a do resistor é , então:
Mas a corrente é simplesmente a derivada da carga em relação ao tempo. Então:
Agora é só resolver essa equação diferencial para encontrar a carga em função do tempo.
Passo 6
O primeiro passo é resolver a equação diferencial homogênea, ou seja, ignorando os termos constantes:
Reorganizando um pouco:
Agora é só integrar dos dois lados:
A integral da esquerda vai dar no , e a da direita vai dar simplesmente (não esqueça de acrescentar a constante):
Aplicando a exponencial dos dois lados:
E a gente pode transformar aquele em uma constante nova:
Beleza, essa é a solução da equação homogênea. Agora temos que encontrar a solução particular da equação inomogênea:
Vamos chutar uma solução constante, do tipo , nesse caso:
Então:
Ok, agora a solução geral é simplesmente a soma dessas duas soluções:
E falta determinar a constante usando uma condição inicial. No nosso caso, como o capacitor começa descarregado, temos , então:
E como :
Então:
Pronto! Deduzimos a fórmula que o enunciado pediu.
Passo 7
Por último, a gente quer saber qual será a carga máxima no capacitor equivalente.
Pra descobrir isso, é só ver o que acontece com a nossa função depois de um tempo muito longo, ou seja:
Quando tende a um valor muito grande, a exponencial vai tender a um valor muito pequeno, então:
Substituindo os valores numéricos:
Resolvido!
Resposta
(a) A resistência equivalente é , a capacitância equivalente é .
(b) As correntes nos resistores são: , e .
(c) A carga no capacitor é dada por .
(d) A carga máxima do capacitor é .