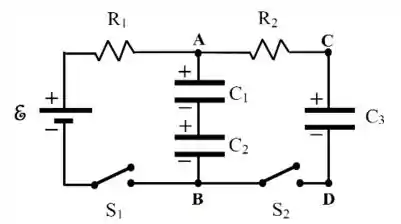
Considere o circuito ao lado, onde os valores de , , , e são conhecidos e os capacitores , e encontram-se inicialmente descarregados. Em seguida, os capacitores e são carregados fechando-se a chave e mantendo-se a chave aberta.
a) Apresente uma expressão para tensão (ddp) no resistor em função do tempo, a partir do instante em que a chave é fechada.
b) Calcule também a energia total armazenada nos dois capacitores e , supondo que a chave permaneceu fechada durante muito tempo.
Agora considere que seja aberta, depois de ter permanecido fechada durante muito tempo. Sabe-se que, neste instante, . Simultaneamente, os capacitores e são conectados ao capacitor descarregado fechando-se a chave que assim permanece durante muito tempo.
c) Calcule as tensões (ddps) finais entre os terminais dos capacitores e .
d) Calcule a energia total armazenada nos capacitores e ao final do processo. Compare com a energia armazenada nos capacitores e imediatamente antes do fechamento da chave . Por que elas são diferentes?
Passo 1
a)
A chave está aberta, então podemos considerar um circuito assim:
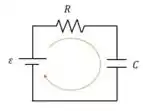
Na figura o representa e a capacitância equivalente entre e . Como esses capacitores estão em série:
Como a chave está fechada, o capacitor está carregando. A equação que descreve a corrente durante o carregamento de um capacitor é:
Além disso,
Substituindo:
Só para ficar mais bonito, podemos definir:
E com isso:
Passo 2
b)
Agora estamos na situação em que ficou fechada muito tempo. E queremos saber a energia armazenada em e .
Se ficou fechada por muito tempo (), quer dizer que o capacitor está completamente carregado. Temos que quando, . Pois
Com isso, , pois
Agora, o capacitor está totalmente carregado, ou seja
A energia armazenada em no capacitor é
Passo 3
c)
Agora nós vamos abrir e fechar Os capacitores e vão se descarregar e o capacitor será carregado.
Além disso, como os capacitores e estão em paralelo com , a tensão nesses terminais será a mesma.
Após se passar muito tempo, , a corrente e a ddp em serão zero. Pelo mesmo motivo que aconteceu na letra a.
Pela conservação de cargas, temos:
representa as cargas que passam pelos capacitores e .ao longo do tempo, representa as cargas no capacitor E no inicio dessa segunda etapa do sistema, toda a carga estava em , que é a capacitância equivalente entre e .. Então, com o decorrer do tempo, temos esse balanço.
Beleza, acompanha aqui comigo. Vimos que a diferença de potencial entre os terminais são iguais. Então, como :
Onde acontece na situação em que está totalmente carregado, mas vimo na letra b que, nesta situação
Então
Então
Como entre os terminais CD temos só o capacitor , então essa é a tensão que procurávamos.
E agora, como falamos, já que os capacitores e ..estão em série, suas cargas são iguais, , ou seja:
Mas
Então, as tensões nos capacitores e valem:
E
Substituindo o valor de
Passo 4
d)
A energia final pé dada pela soma das energia em cada capacitor.
Substituindo o valore de
Mas olha, podemos arrumar um pouquinho:
E como é a energia da primeira etapa, quando estava fechada, vamos chama-la de
Vemos que , isso ocorre porque a diferença de energia entre as etapas foi utilizada na transferência de parte da carga final da primeira etapa, para o capacitor .
Resposta
a)
b)
c)
d)
, isso ocorre porque a diferença de energia entre as etapas foi utilizada na transferência de parte da carga final da primeira etapa, para o capacitor .