No circuito da figura, a fonte tem e resistência interna , as resistências dos resistores são , e , e as capacitâncias dos capacitores são e .
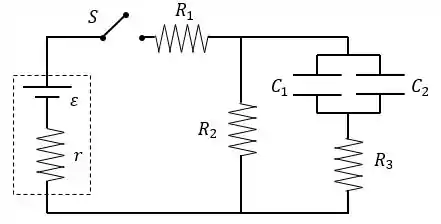
A chave permaneceu fechada por um tempo suficientemente longo para que os capacitores se carregassem totalmente. Nessa situação, calcule:
a corrente através da fonte;
a carga dos capacitores e ;
a diferença de potencial através de .
Com os capacites totalmente carregados, abre-se a chave .
Qual é a energia total dissipada no circuito?
Passo 1
Calcule a corrente através da fonte;
Como os capacitores estão carregados, não há corrente passando por eles. Dessa forma, o circuito pode ser simplificado para:
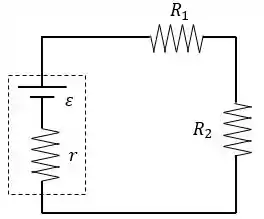
Assim, utilizando a Lei das Malhas de Kirchhoff, teremos:
Passo 2
Calcule a carga dos capacitores e ;
Para os dois circuitos em paralelo, a capacitância equivalente será dada por:
Esse capacitor equivalente possui uma carga , que será dada por:
Que são justamente os caras que queremos calcular.
Agora se liga, o capacitor equivalente e o resistor estão em paralelo com e portanto é necessário que tenham a mesma ddp.
Mas o resistor não terá ddp, portanto a ddp do capacitor equivalente é igual a de .
Isso vai acontecer, pois o capacitor após se carregar não permite a passagem de corrente, logo não há corrente passando por e portanto não há ddp em (Para um resistor, é necessário ter corrente para que haja ddp, beleza?)
Logo:
Substituindo aqui as expressões de e , teremos:
Passo 3
Para calcular as cargas de cada capacitor, temos que, como os mesmos estão em paralelo:
Sendo assim:
Substituindo nas expressões a carga que encontramos no Passo 2, teremos:
Passo 4
Calcule a diferença de potencial através de .
Como não há corrente passando por nessa situação:
Passo 5
Qual é a energia total dissipada no circuito?
Ao abrirmos a chave, o circuito terá essa cara:
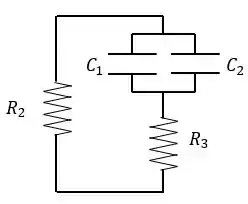
Dessa forma, os capacitores passarão utilizar a energia armazenada pra alimentar o circuito. Dessa forma, a energia dissipada pelos resistores será igual à energia inicialmente armazenada nos resistores, dada por:
Arrumando a casa, teremos o seguinte:
Resposta