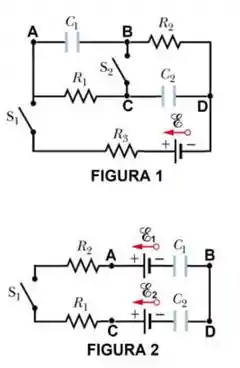
Considere o circuito da Figura 1, onde os valores de , são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e as chaves e abertas. Os capacitores e são carregados fechando-se as duas chaves simultaneamente. Em função dos dados do problema:
a) Apresente expressões para as tensões V1 e V2 e para as energias e armazenadas nos respectivos capacitores, supondo que ambas as chaves permaneceram fechadas durante muito tempo. Considere agora o circuito da Figura 2, onde os valores de , e são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e a chave S1 aberta. No instante , a chave é fechada e assim permanece por muito tempo. Em função dos dados deste novo problema:
b) Apresente expressões para as cargas nos capacitores e em função do tempo.
c) Apresente uma expressão para a tensão no resistor R1 em função do tempo.
d) Apresente expressões para as tensões e em função do tempo.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (a):
Quando a chave é fechada por muito tempo, a corrente deixa de passar pelos capacitores e temos um circuito simples de uma fonte e três resistores em série.
Daí pela lei das malhas temos:
Quando o circuito é em série, a corrente é igual em todo o fio, sendo assim a tensão em é:
E esse resistor é paralelo ao capacitor , logo eles têm a mesma :
Da mesma forma, o resistor é paralelo ao capacitor , então eles também têm a mesma :
E as energias?
Aqui é só aplicar a fórmula, já que sabemos as tensões nos capacitores:
E para o capacitor :
Beleza até aqui?
Passo 2
Letra (b):
O circuito da figura 2 pode ser simplificado com fonte equivalente, capacitância equivalente e resistência equivalente. Vamos começar pela fonte, como elas são opostas temos:
Para a resistência temos:
E para a capacitância temos:
E o valor de :
E como estamos na situação de carregamento, as equações para a carga e para a corrente (que são iguais para os capacitores em série) em função do tempo são:
Substituindo pelas expressões equivalentes temos as expressões mais gerais:
Agora podemos calcular a carga em cada capacitor:
Passo 3
Letra (c):
A tensão em é (aqui vou resgatar a corrente do passo anterior):
Passo 4
Letra (d):
Usando a lei das malhas temos:
E agora fazendo de forma similar para achar :
Espero ter ajudado!