No circuito da figura abaixo, o capacitor está inicialmente descarregado.
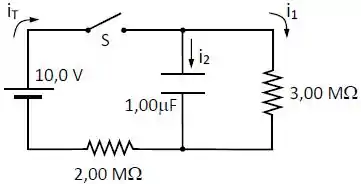
Em a chave é fechada.
Determine as correntes , e em .
Determine as correntes , e para .
Determine a carga no capacitor para .
Suponha agora que a corrente e a carga sejam dadas por
Use os resultados anteriores para determinar as constantes .
Passo 1
Durante o carregamento do capacitor a corrente no mesmo varia da seguinte forma:
- Quando , ... que é o momento imediatamente após a corrente começar a passar pelo capacitor, se trata da corrente máxima que passa por ele.
- Quando , ... ou seja, quando o capacitor fica completamente carregado, a corrente simplesmente para de passar por ele.
Agora podemos começar a quebrar a cabeça.
Passo 2
Determine as correntes , e em .
Como vimos no Passo 1, nesse instante, toda a corrente passa pelo capacitor, logo:
Passo 3
Determine as correntes , e para .
Como vimos no Passo 1, quando , a corrente para de passar pelo capacitor, logo:
Aplicando a Lei das Malhas na malha externa, teremos:
Passo 4
Determine a carga no capacitor para .
A carga no capacitor é dada pela equação:
Como o capacitor está em paralelo com o resistor de , ambos tem a mesma ddp. Logo:
Substituindo na primeira equação, teremos:
Passo 5
Suponha agora que a corrente e a carga sejam dadas por
Use os resultados anteriores para determinar as constantes .
Agora basta aplicar às equações as relações que encontramos nos Passos anteriores.
- :
- :
Passo 6
Passo 7
A corrente no capacitor num tempo é dada por
Já que que tá em série com o capacitor.
Comparando com , vamos ter
Tem unidade de por que o argumento da exponencial é adimensional, então é adimensional quando tem a unidade inversa de .
Resposta