O circuito da Figura 1 abaixo é formado pelos elementos: , , , , e . Adicionalmente, apresenta as seguintes condições iniciais: chave aberta e capacitor descarregado.
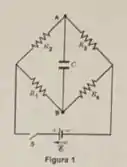
- Determine a corrente na bateria (indicando seu sentido) imediatamente após o fechamento da chave .
- Determine a diferença entre os potenciais , supondo que o capacitor está plenamente carregado.
- Após o pleno carregamento do capacitor, a chave é aberta. Determine a expressão para a diferença entre os potenciais em função do tempo, calculando seus valores numéricos. Indique o sentido da corrente no capacitor.
Passo 1
a) Para o instante de tempo inicial (), o capacitor está inicialmente descarregado , o que significa que a ddp entre os terminais do capacitor também é zero, já que temos
Como , então os pontos e nesse caso terão o mesmo valor. Por isso, os resistores e estão submetidos ao mesmo potencial e, portanto, estão em paralelo. Pela mesma razão, e também estão em paralelo.
A resistência equivalente entre e estará em série com a resistência equivalente entre e . Por isso, a resistência equivalente total será igual a
Portanto, a corrente em será
Passo 2
b) Em um tempo suficientemente grande , o capacitor estará totalmente carregado e por ele não passará nenhuma corrente. Por isso, nessa situação, o resistor estará em série com e estará em série com .
Nesse caso, a resistência equivalente entre e estará em paralelo com a resistência equivalente entre e .
Então, a resistência equivalente total será
Isso vai dar o seguinte para a corrente em (tempo muito grande):
Como a resistência equivalente na parte de cima do circuito é e embaixo é igual a , a corrente que passa por e é , sendo que é a corrente que passa pelos resistores e .
Por isso, podemos aplicar a lei dos Nós no nó da figura e escrever que
Portanto, .
Como temos os valores das correntes, podemos escrever o seguinte sistema entre os pontos e e entre e da figura acima
Subtraindo a primeira equação acima da segunda, vamos obter que
Passo 3
c) Depois desse tempo muito grande, o capacitor estará totalmente carregado e, depois que a chave for aberta, esta carga vai começar a diminuir com o tempo. Consequentemente, a ddp também vai diminuir com o tempo, e é esse comportamento com o tempo de que vamos encontrar agora.
Quando a chave for aberta, não precisaremos mais considerar o trecho que contém a fonte . Basta olhar para as malhas à esquerda do capacitor, por onde passa uma corrente , e a malha à direita de , por onde passa uma corrente .
A corrente que passa pelo capacitor é e, nessa nova situação, os resistores e estão série assim como os resistores e .
Pela lei dos Nós, a corrente do capacitor é igual a
Agora, vamos aplicar a lei das Malhas para as malhas da esquerda e da direita, começando do ponto e retornando a ele somando as diferenças de potencial:
Subtraindo uma equação acima da outra, vamos ter que
Substituindo isso na expressão que obtivemos a partir da lei dos nós, teremos
Do sistema acima, obtido a partir da lei das Malhas, podemos isolar a corrente e substituir em acima
Quando a gente resolve essa integral, vamos chegar a
com
Para obter o potencial , basta dividir por :
sendo que
é a ddp que encontramos no Passo 2.
Como o capacitor está se descarregando, então a corrente que passa por ele está no sentido de baixo para cima e as correntes e estão ambas no sentido anti-horário nas respectivas malhas.