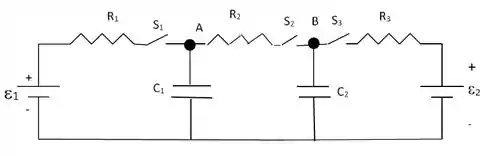
Considere o circuito da figura onde , , , , , e . Os capacitores são de placas planas e paralelas separadas de e têm capacitâncias dadas por . Todos os capacitores estão inicialmente descarregados. Neste circuito, ocorrem as seguintes fases sucessivas:
Fase 1: chaves e fechadas simultaneamente e aberta durante um longo tempo.
Fase 2: chaves , e abertas e, a seguir, a separação das placas de é triplicada e a de é duplicada.
Fase 3: chaves e abertas e fechada durante um longo tempo
Determine:
- A diferença de potencial em função do tempo durante a Fase 1
- A energia armazenada nos capacitores no final da fase 2
- A intensidade e sentido da corrente em no início da fase 3
- O trabalho necessário para aumentar a separação das placas do capacitor e a força externa mínima (sem aceleração) na Fase 2. (Sugestão: lembre-se que , sendo a distância entre as placas)
Passo 1
Quando a chave está aberta e as chaves e estão fechadas, teremos duas malhas, uma na esquerda e outra na direita.
Olhando para a malha da esquerda, temos
Que é a equação de um circuito . Nesse caso a voltagem no capacitor é dada por
Onde
Como
Olhando para a malha da direita, temos
Que é a equação de um circuito . Nesse caso a voltagem no capacitor é dada por
Onde
Como
Olhando para o circuito vemos que as voltagens e são dadas por
De forma que a diferença é dada por
Passo 2
Vamos lembrar da energia potencial de um capacitor
Ou seja, precisamos da capacitância e da carga em cada um dos capacitores!
Agora vamos lembrar de uma coisa! Na fase 1 carregamos nossos capacitores totalmente (isso por que se passou um tempo longo).
Como na fase 2 abrimos todas as chaves, os nossos capacitores não irão se descarregar. Dessa forma temos que a voltagem em cada um dos capacitores será igual à voltagem das suas respectivas fontes de tensão.
Temos então (antes de mudarmos os capacitores)
E para o segundo capacitor, temos
Passo 3
Beleza, beleza!
Agora vamos ver como as capacitâncias são alteradas depois de mudarmos a distância entre suas placas.
A capacitância é dada por
No primeiro capacitor triplicamos a distância entre as placas, isso quer dizer que sua nova capacitância é um terço da capacitância original
No segundo capacitor duplicamos a distância entre as placas, isso quer dizer que sua nova capacitância é metade da capacitância original
Passo 4
Show! Agora é só calcular a energia potencial! Só que vamos usar as capacitâncias modificadas, fica ligado!
A energia no capacitor será
A energia no capacitor será
Passo 5
Na fase 3 as chaves e estarão abertas e a chave estará fechada, o que faz com que tenhamos uma malha no meio com os dois capacitores totalmente carregados, e , e a resistência .
O capacitor estava ligado à fonte e sua polarização será tal que a placa de cima terá carga positiva e a de baixo terá carga negativa e a mesma coisa acontecerá no capacitor (que estava ligado à fonte ).
Assim usando a lei das malhas, supondo a corrente no sentido anti-horário
Como queremos saber a corrente no início da fase 3, onde os capacitores estão totalmente carregados, basta usar os valores de e dos passos anteriores. Assim
Como achamos a corrente positiva, isso indica que a corrente está no sentido anti-horário.
Passo 6
Na fase 2 aumentamos a distância das placas do capacitor de para , mudando a capacitância de para e mantendo a carga do capacitor.
O trabalho para fazer essa mudança é dado
Temos que a energia de potencial em um capacitor é dada por
Como a capacitância é dada por , chamando de a distância entre as placas
Temos que a derivada da energia potencial se relaciona com a força por
Já sabemos no capacitor a carga , agora pasta saber quanto vale . Isso é facilmente resolvido lembrando que
Quando a distância entre as placas é temos que a capacitância é (você poderia usar e o valor de ), assim
(em unidades do SI)
Assim
Resposta
(a)
(b) e
(c) no sentido anti-horário.
(d) e