Em algum ponto da trajetória de determinada partícula, os vetores velocidade e aceleração são dados pelo diagrama abaixo.
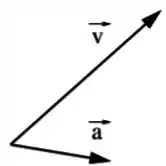
Dada a trajetória abaixo, determine que ponto da trajetória é compatível com este diagrama.
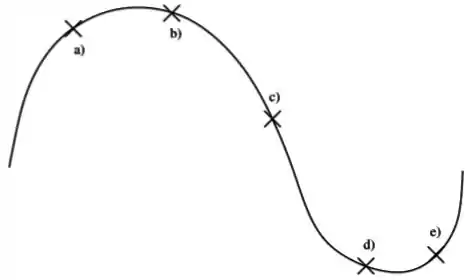
Passo 1
Legal, temos aqui a trajetória da partícula, que pode ser interpretado também como posição da partícula ao longo do tempo. Lembra que a velocidade é a derivada em relação ao tempo da posição? Então, a interpretação geométrica da derivada é a inclinação das retas tangentes às curvas. Vou desenhar a reta tangente em cada ponto, ou seja, a direção da velocidade em cada ponto.
Então, Com esse desenho vemos que as únicas opções possíveis são as alternativas e , então vamos agora analisar a aceleração.
Nos pontos e temos um movimento circular não é mesmo? Lembra como era a aceleração em movimentos circulares? Elas costumam apontar para o centro da curva, é a famosa aceleração centrípeta! Vamos desenhá-las então:
Agora sim, achamos que o ponto é compatível com o diagrama.
Resposta
Alternativa