UFRJ – Física 1 – P1 – 2019.2 – Questão 2
Uma bolinha, presa a uma das extremidades de um fio ideal tenso, gira em um plano vertical descrevendo uma circunferência. A velocidade da bolinha tem módulo constante. Quando o fio está na horizontal, a tração nele tem módulo igual a oito vezes o módulo do peso da bolinha. Podemos dizer que a razão entre as trações no fio nos pontos mais alto e mais baixo da trajetória circular da bolinha é
Passo 1
Vamos lá! Ele quer descobrir a razão entre a tração no ponto mais alto e a tração no ponto mais baixo.
Podemos começar esboçando um desenho do problema
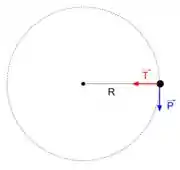
Verificando as forças que atuam sobre a bolinha quando esta se encontra na horizontal temos que, como estamos tratando de um movimento circular, haverá uma resultante centrípeta que aponta para o centro da circunferência. Sendo assim,
O enunciado diz que, quando a bolinha está na horizontal, a tração é
Passo 2
Como a bolinha tem módulo constante, a força centrípeta será a mesma em todos os pontos.
Vamos verificar as forças quando a bolinha está no ponto mais baixo. Se liga na figura!
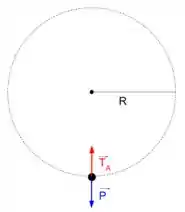
Como a força centrípeta é a resultante das forças, podemos escrever que
Passo 3
Agora vamos verificar o que ocorre com a bolinha no ponto mais alto.
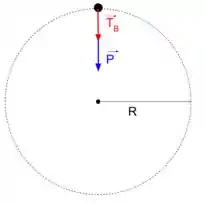
Pelas forças descritas na figura, temos
Passo 4
Como ele quer a razão entre a tração da bolinha no ponto mais alto e a bolinha no ponto no ponto mais baixo, temos
Sendo assim, a resposta é a alternativa (d).