Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
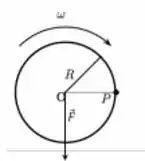
A figura abaixo representa um disco de massa M homogêneo e uniforme, de espessura desprezível, e raio R. O disco gira no sentido horário em torno do seu eixo de simetria, com velocidade angular constante de módulo ω, e move-se sob a ação da força F mantendo-se sempre num mesmo plano. Sabendo-se que a aceleração do centro de massa do disco é devida apenas a ação da força F, o módulo da aceleração do ponto P localizado na borda do disco, mostrado na figura, é:
Passo 1
Como a questão nos disse, a aceleração do centro de massa do disco se deve apenas a essa força, então primeiro a gente tem:
Beleza, então essa é a aceleração do centro de massa, né? Show! Mas esse disco também tá girando, então ele vai ter uma aceleração centrípeta também, ou seja:
Como temos duas componentes do vetor aceleração, vamos usar aquela regrinha pra calcular o módulo do vetor, então temos:
O que nos deixa com a letra a como resposta!