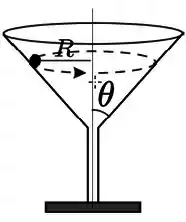
Uma partícula de massa está dentro de um funil de vidro e percorre a sua superfície inferior com um movimento circular uniforme horizontal. Não há atrito entre a parede do funil e a partícula. O ângulo que a parede do funil faz com o seu eixo de simetria é igual a , como mostra a figura. Desprezando a presença do ar, o módulo da força da superfície sobre a partícula e o módulo da aceleração centrípeta da partícula são, respectivamente,
- e
- e
- e
- e
- e
Passo 1
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dela é considerada?
- Ela está encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ela tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
Não, não existe atrito
O DCL da partícula fica
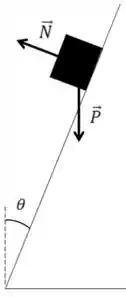
Nesse caso, por mais que estejamos em um plano inclinado, como ela está rodando é importante determinarmos a resultante na direção do centro da curva. E como ele pretende que ela não caia é melhor, neste caso, usarmos os em relação ao chão e não em relação à superfície inclinada.
Estão mega confusas essas forças né? Vamos tentar ver em um esquema melhor.
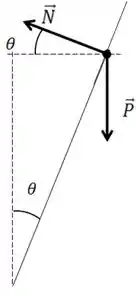
Como fizemos essa mudança de ângulo?
Vamos chamar de o ângulo entre o eixo horizontal e a superfície inclinada.
Consegue perceber que
Soma dos ângulos internos de um triangulo certo? O que isso nos diz?
Repare que o ângulo que a normal faz com o eixo horizontal somado com é igual a . Então esse ângulo deve ser , pela fórmula ali em cima.
Voltando à física.
Passo 2
Vamos fazer o equilíbrio no
Vamos achar a componente da , usando a “regra do COlado, SEparado”.
Teremos então
Passo 3
Vamos agora ao
Sabemos que o módulo da força centrípeta deve ser igual ao módulo na componente da normal. Vamos achar o módulo de
Passo 4
Teremos então
Diferentemente do normal, escrevemos a força centrípeta assim porque o que ele quer é a aceleração centripeta mesmo, não a velocidade.
Passo 5
Vamos só reescrever aqui o que achamos
Resposta
Letra E