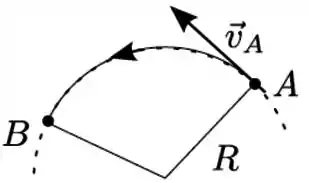
Uma partícula percorre uma trajetória circular de raio onde, no trecho do arco , o módulo da sua velocidade é reduzido uniformemente, isto é, com derivada constante. No ponto a sua velocidade é , conforme ilustrado na figura. Considere a sua aceleração decomposta segundo duas direções, um componente na direção radial (aceleração radial) e o outro componente na direção tangente à trajetória (aceleração tangencial). No seu movimento de para a afirmativa correta é
(a) a aceleração tem módulo constante;
(b) a aceleração radial tem módulo constante;
(c) a aceleração tangencial tem módulo constante;
(d) a aceleração tangencial é sempre nula;
(e) nenhuma das respostas anteriores.
Passo 1
A aceleração radial (ou centrípeta) é que faz a mudança de direção da partícula na curva, mas ela não tem nenhuma influência na sua velocidade. Quem altera o módulo da velocidade da partícula é a aceleração tangencial!
Passo 2
O módulo da velocidade está sendo reduzido de maneira uniforme, então isso significa que o módulo da aceleração tangencial é constante (e não nulo).
Observação: o módulo da aceleração radial é dado por , então como a velocidade está diminuindo, esse módulo também diminui. Por isso podemos eliminar as alternativas (a) e (b).
Resposta
Alternativa (c)