Um carro de massa descreve sem derrapar uma curva no plano horizontal de raio com velocidade . O gráfico ao lado indica o comportamento da força de atrito para este caso específico.
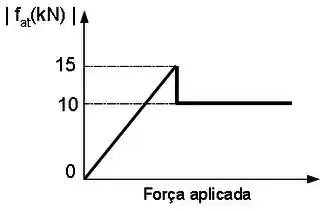
(a) Determine o módulo da força de atrito que atua no carro neste momento.
Passo 1
Analisar o movimento do carro
Antes de mais nada, vamos das uma olhada no movimento do carro:
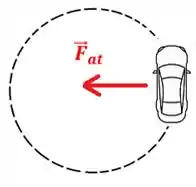
No movimento circular do carro, a nossa querida força de atrito vai atuar como uma força centrípeta, beleza? Se é assim, podemos igualar as duas:
Passo 2
Fazer as contas
Antes de substituir, vamos tomar um cuidado aqui! Fica esperto que o enunciado deu a velocidade em ! A velocidade do carro então, pra , basta dividir por tá? Então vamos usar ao invés de pra que a força já saia com unidade de Newtons: