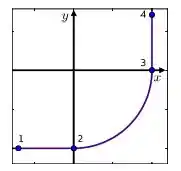
Parte de uma ferrovia é composta por dois trechos retilíneos mutuamente ortogonais conectados por um arco de circunferência conforme mostrado na figura abaixo. Uma locomotiva percorre a ferrovia no sentido do ponto ao ponto com velocidade de módulo constante.
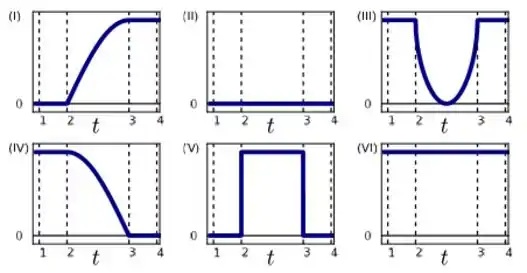
Considere, então, os trechos abaixo, em que o tempo é representado no eixo horizontal, enquanto no eixo vertical encontra-se alguma função de . Assinale a alternativa que lista corretamente os trechos correspondentes à componente da velocidade, à componente da velocidade, ao módulo da aceleração e à aceleração tangencial, respectivamente, da locomotiva em função de :
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Vamos fazer o seguinte: para cada função de dita no enunciado a gente vai vendo quais propriedades o gráfico tem que ter, beleza?
- Componente da velocidade
Entre os pontos 1 e 2, todo o módulo da velocidade está no eixo , portanto, o gráfico deve ser uma reta horizontal em um valor maior que zero.
Entre os pontos 2 e 3, temos que:
E então:
O que nos mostra que a componente vai caindo a medida que a componente vai aumentando. Esta queda segue uma parábola!
Entre os pontos 3 e 4, a velocidade não tem componente , portanto, o gráfico deve ser constante e igual a zero.
Vemos então que somente o gráfico IV atende essas propriedades.
Passo 2
- Componente da velocidade
Entre os pontos 1 e 2, a velocidade não tem componente , portanto, o gráfico deve ser constante e igual a zero.
Entre os pontos 2 e 3, temos que:
E então:
O que nos mostra que a componente vai crescendo a medida que a componente vai caindo. Esta subida segue uma parábola!
Entre os pontos 1 e 2, todo o módulo da velocidade está no eixo , portanto, o gráfico deve ser uma reta horizontal em um valor maior que zero.
Vemos então que somente o gráfico I atende essas propriedades.
Passo 3
- Módulo da aceleração
Como a velocidade tem módulo constante, só existe aceleração no trecho onde ela muda de direção, ou seja, entre os pontos 2 e 3.
A aceleração neste trecho é constante e igual a aceleração centrípeta. Fora deste trecho, os gráficos devem ser constantes e iguais a zero.
Vemos então que somente o gráfico V atende essas propriedades
Passo 4
- Aceleração tangencial
Vimos que só no trecho entre os pontos 2 e 3 possui aceleração, e essa aceleração é completamente radial. Portanto, a aceleração tangencial é, durante todo o trecho, nula, o que é mostrado no gráfico II
Todas essas análises nos mostram que a reposta certa é a letra (c)
Resposta
Letra (c)