Um corpo de massa é abandonado do alto de um plano inclinado (1), que possui altura em relação ao solo, e percorre seu comprimento livre de forças de atrito até entrar em um movimento de “loop” (2), conforme mostra a figura. Use para a aceleração da gravidade.
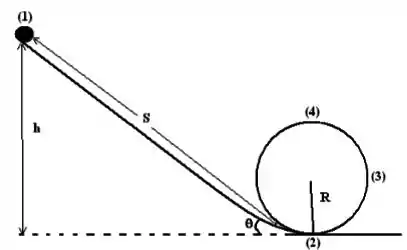
a) Utilizando um eixo de coordenadas com a direção paralela ao plano inclinado, represente o diagrama de corpo livre para a situação na qual o corpo se encontra na posição (1) e descreva, a partir da segunda lei de Newton, as componentes das forças que atuam no corpo para cada eixo.
b) Escreva a expressão para a velocidade em função da altura de lanamento com que o corpo chega à posição (2) indicada na figura.
c) Escreva a segunda lei de Newton por componentes para a situação na qual o corpo se encontra na posição (4) com velocidade e obtenha uma expressão para a altura mínima , em função do raio , de onde o corpo deve ser lançado para que consiga completar a volta no loop.
d) Considerando que o corpo abandonado de uma altura e o loop tem um raio , sua velocidade no ponto (3) é . Calcule os módulos e direções da força normal e da força resultante que atuam no corpo ao passar naquele ponto. Use .
Passo 1
a)
O diagrama de corpo livre ficará:
Aplicando a segunda lei no eixo :
Aplicando a segunda lei no eixo :
Como a bola não se movimenta no eixo , . Logo:
Passo 2
b)
Na direção do plano, podemos aplicar a fórmula:
Substituindo:
Entretanto a questão não quer a velocidade em função do comprimento da rampa. Ele quer em função da altura. Mas podemos relacionar eles por:
Agora é só substituir:
Passo 3
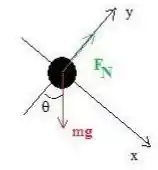
c)
Na posição (4), podemos fazer o seguinte diagrama de forças.

Aplicando a segunda lei por componentes:
No eixo :
No eixo :
Lembrando que a força resultante é a força centrípeta. Então podemos substituir essa aceleração por:
Substituindo a fórmula da aceleração centrípeta:
Muito bem, no limite para se completar a volta, temos uma velocidade mínima para que o corpo não perca contato com a superfície. Essa velocidade pode ser calculada se nós tendermos a força normal (força de contato com a superfície) à zero. Portanto:
Certo, só que não queremos a velocidade mínima em função do raio, queremos a altura mínima em função do raio. Então vamos usar conservação de energia entre os pontos (1) e (4).
Agora é só substituir a velocidade que encontramos e a altura que é igual a .
Passo 4
d)
Podemos montar o seguinte diagrama de forças:
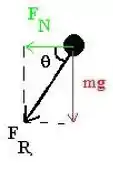
Aplicando a segunda lei de Newton por componentes:
No eixo :
No eixo :
A intensidade da força resultante será:
Direção:
Resposta
a)
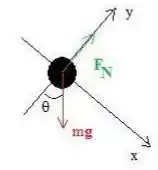
b)
c)
d)
Direção horizontal.