Uma moeda de massa repousa sobre um bloco de massa . Ambos estão sobre uma plataforma circular de raio que gira com 60 rotaçoes por minuto em torno de um eixo na direção vertical. Os coeficientes de atrito estático e cinético entre o bloco e a plataforma são respectivamente e . O coeficiente de atrito estático e cinético entre a moeda e o bloco são respectivamente e . Use e .
Calcule as forças centrípetas que atuam na moeda e no bloco.
Faça um diagrama de corpo livre da moeda e do bloco e indique (se houver) os pares ação-reação.
Calcule a força de atrito que atua entre o bloco e a plataforma.
Qual é a máxima rotação por minuto que a plataforma pode ter antes que o bloco ou a moeda caiam da plataforma.
Passo 1
Para calcular as forças centrípetas, vamos primeiro relembrar da seguinte fórmula:
Podemos descobrir a velocidade dos corpos, pois ele nos diz quantas rotações são efetuadas por minuto, e sabemos o valor do raio, temos, então:
Sabendo que são realizadas rotações por minuto, temos que cada rotação é feita em um segundo! Desse modo, temos, para a velocidade:
Agora podemos calcular a força centrípeta de cada corpo!
Passo 2
Para o bloco, temos:
Para a moeda, temos:
Passo 3
Vamos analisar cada corpo em separado:
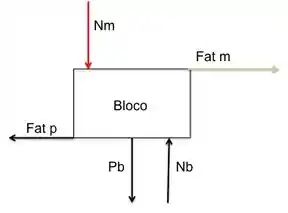
Começando pelo bloco, podemos ver que nele atuam:
- força peso
- normal da plataforma , que sustenta o peso
- força de atrito entre a plataforma e o bloco
- normal da moeda
- força de atrito entre o bloco e a moeda
Parece muita coisa....mas dá uma olhada no desenho abaixo!
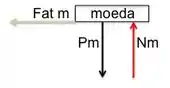
Agora, analisando a moeda, vemos que atuam:
- força peso da moeda
- normal do bloco , que sustenta o peso da moeda
- força de atrito entre a moeda e o bloco
Se liga!
Das forças que atuam nos corpos, temos somente dois pares de ação e reação, a força de atrito entre o bloco e a moeda, veja que temos a mesma força de atrito em módulo atuando nos dois corpos. Além desse par, temos o par da normal da moeda, atuando na moeda e no bloco.
Passo 4
Como já calculamos a força centrípeta que atua em cada corpo, para calcular a força de atrito entre a plataforma e bloco, precisamos fazer:
Como sabemos que:
Substituindo, temos:
Isolando a força de atrito que queremos descobrir, temos:
Passo 5
Para descobrir a velocidade máxima de rotação, precisamos pensar que essa rotação máxima está limitada pela força de atrito. Analisando os coeficientes de atrito e a normal que atua em cada corpo, vemos que a menor força de atrito é aquela entre o bloco e a moeda.
Portanto, a velocidade máxima está limitada pela força de atrito entre o bloco e a moeda. Dessa maneira, temos:
Substituindo os valores, temos:
Agora é só transformar em revoluções por minuto!
Resposta
;
Ver figuras acima