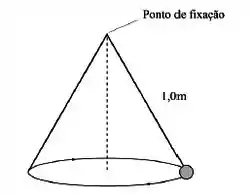
Um “pêndulo cônico” é formado por uma bola de presa a um barbante de de comprimento, fazendo com que a massa se mova em um círculo horizontal com de raio. A figura abaixo mostra que, ao girar, o barbante descreve a superfície de um cone imaginário, daí o nome do dispositivo. Quanto vale a velocidade angular da bola?
(A)
(B)
(C)
(D)
(E)
Passo 1
A bola faz um movimento circular uniforme na base do “cone”.
O caminho para achar essa velocidade angular é relacionar a força de tração na corda com a força centrípeta.
Passo 2
Vamos olhar para as forças na bola:
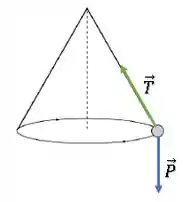
Como nós temos as dimensões do pêndulo e do raio, podemos decompor a força de Tração a partir do ângulo de abertura do pêndulo.
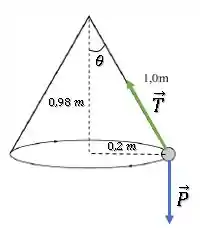
Temos que:
Decompondo a força de Tração:
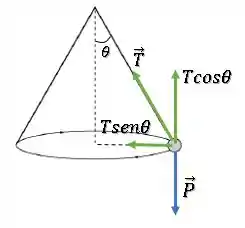
A bola está em equilíbrio na vertical, então:
A componente horizontal, aponta para o centro da trajetória circular da bola, então, ela age como uma força centrípeta. Assim, podemos dizer que:
Podemos juntar as duas equações dividindo (2) por (1):
Passo 3
Já conseguimos encontrar a velocidade linear da partícula, porém, queremos a velocidade angular .
Lembra daquela relação de movimento circular?
Essa tem que estar no sangue hahah.
Podemos substituir na equação:
Substituindo os valores, achamos que:
Então, achamos que a velocidade angular é aproximadamente:
Ficamos com a alternativa (e).
Resposta
Letra (e)